天津市和平区2016-2017年中考三模数学考试试卷
试卷更新日期:2017-08-23 类型:中考模拟
一、选择题
-
1. 计算﹣42的结果等于( )A、﹣16 B、16 C、﹣8 D、82. 计算 cos30°的值为( )A、 B、 C、1 D、33. 下列图案中,轴对称图形的个数有( )
 A、1个 B、2个 C、3个 D、4个4. “厉行勤俭节约,反对铺张浪费”势在必行,最新统计数据显示,中国每年浪费食物总量折合粮食大约是230000000人一年的口粮,将230000000用科学记数法表示为( )A、2.3×109 B、0.23×109 C、2.3×108 D、23×1075. 如图是由3个相同的正方体组成的一个立方体图形,它的三视图是( )
A、1个 B、2个 C、3个 D、4个4. “厉行勤俭节约,反对铺张浪费”势在必行,最新统计数据显示,中国每年浪费食物总量折合粮食大约是230000000人一年的口粮,将230000000用科学记数法表示为( )A、2.3×109 B、0.23×109 C、2.3×108 D、23×1075. 如图是由3个相同的正方体组成的一个立方体图形,它的三视图是( )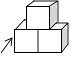 A、
A、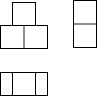 B、
B、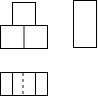 C、
C、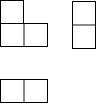 D、
D、 6. 某种植物的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支,主干、枝干和小分支的总数是91.设每个枝干长出x个小分支,则x满足的关系式为( )A、x+x2=91 B、1+x2=91 C、1+x+x2=91 D、1+x(x﹣1)=917. 二次根式 中x的取值范围是( )A、x>3 B、x≤3且x≠0 C、x≤3 D、x<3且x≠08. 若两个非零的有理数a,b满足:|a|=﹣a,|b|=b,a+b<0,则在数轴上表示数a,b的点正确的是( )A、
6. 某种植物的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支,主干、枝干和小分支的总数是91.设每个枝干长出x个小分支,则x满足的关系式为( )A、x+x2=91 B、1+x2=91 C、1+x+x2=91 D、1+x(x﹣1)=917. 二次根式 中x的取值范围是( )A、x>3 B、x≤3且x≠0 C、x≤3 D、x<3且x≠08. 若两个非零的有理数a,b满足:|a|=﹣a,|b|=b,a+b<0,则在数轴上表示数a,b的点正确的是( )A、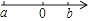 B、
B、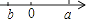 C、
C、 D、
D、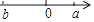 9. 如图,直线y1= x+2与双曲线y2= 交于A(2,m)、B(﹣6,n)两点,则当y1<y2时,x的取值范围是( )
9. 如图,直线y1= x+2与双曲线y2= 交于A(2,m)、B(﹣6,n)两点,则当y1<y2时,x的取值范围是( )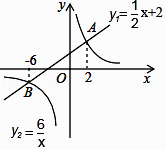 A、x<﹣6或x>2 B、﹣6<x<0或x>2 C、x<﹣6或0<x<2 D、﹣6<x<210. 如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠B的度数是( )
A、x<﹣6或x>2 B、﹣6<x<0或x>2 C、x<﹣6或0<x<2 D、﹣6<x<210. 如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠B的度数是( )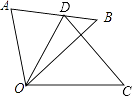 A、40° B、35° C、30° D、15°11. 如图,△ABC和△DEF分别是⊙O的外切正三角形和内接正三角形,则它们的面积比为( )
A、40° B、35° C、30° D、15°11. 如图,△ABC和△DEF分别是⊙O的外切正三角形和内接正三角形,则它们的面积比为( )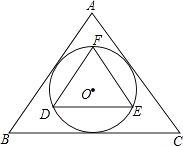 A、4 B、2 C、 D、12. 已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:
A、4 B、2 C、 D、12. 已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a﹣b+c≥0;
④ 的最小值为3.
其中,正确结论的个数为( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 计算﹣x2•x5的结果等于 .14. 计算 的结果等于 .15. 在单词mathematics(数学)中任意选择一个字母,选中字母“a”的概率为 .16. 如果反比例函数y= (a为常数)的图象,在每一个象限内,y随x的增大而减小,写出一个符合条件的a的值为 .17.
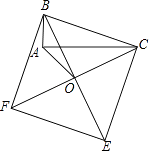
如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6 ,那么AC= .
 18.
18.如图,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上.
 (1)、S△ABC=;(2)、请在如图所示的网格中,用无刻度的直尺,画出一个以AB为底边的等腰△ABP,使该三角形的面积等于△ABC的面积,并简要说明点P的位置是如何找到的(不要求证明) .
(1)、S△ABC=;(2)、请在如图所示的网格中,用无刻度的直尺,画出一个以AB为底边的等腰△ABP,使该三角形的面积等于△ABC的面积,并简要说明点P的位置是如何找到的(不要求证明) .
三、解答题
-
19. 解不等式组 .请结合题意填空,完成本题的解答.(1)、解不等式①,得:;(2)、解不等式②,得:;(3)、把不等式①和②的解集在数轴上表示出来;
 (4)、不等式组的解集为: .20.
(4)、不等式组的解集为: .20.中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽取了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
 (1)、写出扇形图中a=%,并补全条形图;(2)、求本次调查获取的样本数据的平均数,众数和中位数;(3)、该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?21. 在△ABC中,AB=AC,以AB为直径的⊙O分别交边BC、AC于点D、点E,且AE=BE.(1)、如图①,求∠EBC的度数;
(1)、写出扇形图中a=%,并补全条形图;(2)、求本次调查获取的样本数据的平均数,众数和中位数;(3)、该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?21. 在△ABC中,AB=AC,以AB为直径的⊙O分别交边BC、AC于点D、点E,且AE=BE.(1)、如图①,求∠EBC的度数;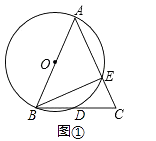 (2)、如图②,过点D作⊙O的切线交AB的延长线于点G,交AC于点F,若⊙O的直径为10,求BG的长.
(2)、如图②,过点D作⊙O的切线交AB的延长线于点G,交AC于点F,若⊙O的直径为10,求BG的长.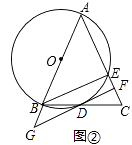 22.
22.如图,大楼AB高16m,远处有一塔CD,某人在楼底B处测得塔顶C的仰角为39°,在楼顶A处测得塔顶的仰角为22°,求塔高CD的高.(结果保留小数后一位)
参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,si39°≈0.63,cos39°≈0.78,tan39°≈0.81.
 23. 某工厂计划招聘A、B两个工种的工人共120人,A、B两个工种的工人月工资分别为3200元和4000元.(1)、若某工厂每月支付的工人工资为440000元,那么A、B两个工种的工人各招聘多少人?设招聘A工种的工人x人,填写下表,并列方程求解.(2)、设工厂每月支付的工人工资y元,试写出y与x之间的函数表达式,若要求B工种的人数不少于A工种人数的2倍,那么招聘A工种的工人多少人时,可使工厂每月支付的工人工资最少?
23. 某工厂计划招聘A、B两个工种的工人共120人,A、B两个工种的工人月工资分别为3200元和4000元.(1)、若某工厂每月支付的工人工资为440000元,那么A、B两个工种的工人各招聘多少人?设招聘A工种的工人x人,填写下表,并列方程求解.(2)、设工厂每月支付的工人工资y元,试写出y与x之间的函数表达式,若要求B工种的人数不少于A工种人数的2倍,那么招聘A工种的工人多少人时,可使工厂每月支付的工人工资最少?工种
工人每月工资(元)
招聘人数
工厂应付工人的约工资(元)
A
3200
x
B
4000
24.将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A( ,0),点B(0,3),点O(0,0)
 (1)、过边OB上的动点D(点D不与点B,O重合)作DE丄OB交AB于点E,沿着DE折叠该纸片,点B落在射线BO上的点F处.
(1)、过边OB上的动点D(点D不与点B,O重合)作DE丄OB交AB于点E,沿着DE折叠该纸片,点B落在射线BO上的点F处.①如图,当D为OB中点时,求E点的坐标;
②连接AF,当△AEF为直角三角形时,求E点坐标;
(2)、P是AB边上的动点(点P不与点B重合),将△AOP沿OP所在的直线折叠,得到△A′OP,连接BA′,当BA′取得最小值时,求P点坐标(直接写出结果即可).25. 二次函数y= (x﹣5)(x+m)(m是常数,m>0)的图象与x轴交于点A和点B(点A在点B的右侧)与y轴交于点C,连接AC.(1)、用含m的代数式表示点B和点C的坐标;(2)、垂直于x轴的直线l在点A与点B之间平行移动,且与抛物线和直线AC分别交于点M、N,设点M的横坐标为t,线段MN的长为p.①当t=2时,求p的值;
②若m≤1,则当t为何值时,p取得最大值,并求出这个最大值.