四川省广元市苍溪县2016-2017学年中考二模数学考试试卷

试卷更新日期：2017-08-23 类型：中考模拟

进入出卷网下载

一、选择题

1. 计算（﹣3）﹣（﹣9）的结果等于（）

A、12 B、﹣12 C、6 D、﹣6

查看试题解析
2. 下列几何体的主视图与其他三个不同的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，在△ABC中，AB=AC，∠BAC=100°，AB的垂直平分线DE分别交AB、BC于点D、E，则∠BAE=（）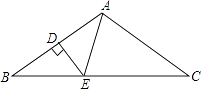

A、80° B、60° C、50° D、40°

查看试题解析
4. 在①﹣a⁵•（﹣a）²；②（﹣a⁶）÷（﹣a³）；③（﹣a²）³•（a³）²；④[﹣（﹣a）²]⁵中计算结果为﹣a¹⁰的有（）

A、①② B、③④ C、②④ D、④

查看试题解析
5. 下列说法中正确的是（）

A、“任意画出一个等边三角形，它是轴对称图象”是随机事件 B、任意掷一枚质地均匀的硬币10次，正面向上的一定是5次 C、“概率为0.0001的事件”是不可能事件 D、“任意画出一个平行四边形，它是中心对称图形”是必然事件

查看试题解析
6. 已知不透明的袋中只装有黑、白两种球，这些球除颜色外都相同，其中白球有2个，黑球有n个，随机地从袋中摸出一个球，记录下颜色后，放回袋子中并摇匀，经过大量重复试验发现摸出白球的频率稳定在0.4附近，则n的值为（）

A、2 B、3 C、4 D、5

查看试题解析
7. 如图，四边形ABCD内接于⊙O，如果它的一个外角∠DCE=64°，那么∠BOD=（）

A、128° B、100° C、64° D、32°

查看试题解析
8.
如图，已知A点坐标为（5，0），直线y=x+b（b＞0）与y轴交于点B，连接AB，∠α=75°，则b的值为（）

A、3 B、 $\frac{5 \sqrt{3}}{3}$ C、4 D、 $\frac{5 \sqrt{3}}{4}$

查看试题解析
9. 已知二次函数y=x²﹣2x﹣3，点P在该函数的图象上，点P到x轴、y轴的距离分别为d₁、d₂ ．设d=d₁+d₂ ，下列结论中：
①d没有最大值；
②d没有最小值；
③﹣1＜x＜3时，d随x的增大而增大；
④满足d=5的点P有四个．
其中正确结论的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

10. 分解因式：m²﹣4= ．

查看试题解析
11. 已知x₁和x₂分别为方程x²+x﹣2=0的两个实数根，那么x₁+x₂=；x₁•x₂= ．

查看试题解析
12. 甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数都是9.2环，方差分别为s_甲²=0.56，s_乙²=0.60，s_丙²=0.50，s_丁²=0.45，则成绩最稳定的是．

查看试题解析
13. 如图，四边形ABCD是⊙O的内接四边形，∠B=137°，则∠AOC的度数为．

查看试题解析
14.
如图，在平面直角坐标系xOy中，平行四边形OABC的顶点A，B的坐标分别为（6，0），（7，3），将平行四边形OABC绕点O逆时针方向旋转得到平行四边形OA′B′C′，当点C′落在BC的延长线上时，线段OA′交BC于点E，则线段C′E的长度为．

查看试题解析

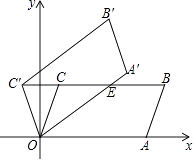
三、计算题

15. 计算： $\sqrt{12}$ +| $\sqrt{3}$ ﹣3|﹣2sin60°﹣（ $\sqrt{3}$ ）²+2016⁰ ．

查看试题解析
16. 先化简，再求值： $\frac{a^{2} + a}{a^{2} - 2 a + 1}$ $\div (\frac{2}{a - 1} - \frac{1}{a})$ ，其中a是方程2x²+x﹣3=0的解．

查看试题解析
17. 如图，贵阳市某中学数学活动小组在学习了“利用三角函数测高”后．选定测量小河对岸一幢建筑物BC的高度．他们先在斜坡上的D处，测得建筑物顶的仰角为30°．且D离地面的高度DE=5m．坡底EA=10m，然后在A处测得建筑物顶B的仰角是50°，点E，A，C在同一水平线上，求建筑物BC的高．（结果保留整数）

查看试题解析
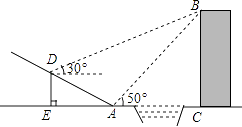18. 如图，一次函数y=kx+b的图象分别与反比例函数y= $\frac{a}{x}$ 的图象在第一象限交于点A（4，3），与y轴的负半轴交于点B，且OA=OB．

(1)、求函数y=kx+b和y= $\frac{a}{x}$ 的表达式；

(2)、已知点C（0，5），试在该一次函数图象上确定一点M，使得MB=MC，求此时点M的坐标．

查看试题解析
19. 如图，在⊙O的内接四边形ACDB中，AB为直径，AC：BC=1：2，点D为弧AB的中点，BE⊥CD垂足为E．

(1)、求∠BCE的度数；

(2)、求证：D为CE的中点；

(3)、连接OE交BC于点F，若AB= $\sqrt{10}$ ，求OE的长度．

查看试题解析
20. 已知甲同学手中藏有三张分别标有数字 $\frac{1}{2}$ 、 $\frac{1}{4}$ 、1的卡片，乙同学手中藏有三张分别标有数字1、3、2的卡片，卡片外形相同．现从甲乙两人手中各任取一张卡片，并将它们的数字分别记为a，b．

(1)、请你用树形图或列表法列出所有可能的结果；

(2)、现制定一个游戏规则：若所选出的a，b能使得ax²+bx+1=0有两个不相等的实数根，则甲获胜；否则乙获胜．请问这样的游戏规则公平吗？请用概率知识解释．

查看试题解析
21. 如图，已知矩形ABCD的两条对角线相交于点O，过点A作AG⊥BD分别交BD、BC于点G、E．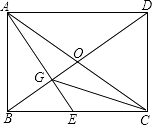

(1)、求证：BE²=EG•EA；

(2)、连接CG，若BE=CE，求证：∠ECG=∠EAC．

查看试题解析
22. 某商场经营某种品牌的玩具，进价是20元，根据市场调查：在一段时间内，销售单价是30元时，销售量是500件，而销售单价每涨1元，就会少售出10件玩具．

(1)、不妨设该种品牌玩具的销售单价为x元（x＞30），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：
销售单价（元）
x
销售量y（件）
销售玩具获得利润w（元）

(2)、在（1）问条件下，若商场获得了8000元销售利润，求该玩具销售单价x应定为多少元．

(3)、在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于35元，且商场要完成不少于350件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？

查看试题解析
23.
如图，长方形OABC的OA边在x轴的正半轴上，OC在y轴的正半轴上，抛物线y=ax²+bx经过点B（1，4）和点E（3，0）两点．

(1)、求抛物线的解析式；

(2)、若点D在线段OC上，且BD⊥DE，BD=DE，求D点的坐标；

(3)、在条件（2）下，在抛物线的对称轴上找一点M，使得△BDM的周长为最小，并求△BDM周长的最小值及此时点M的坐标；

(4)、在条件（2）下，从B点到E点这段抛物线的图象上，是否存在一个点P，使得△PAD的面积最大？若存在，请求出△PAD面积的最大值及此时P点的坐标；若不存在，请说明理由．

查看试题解析

销售单价（元）	x
销售量y（件）
销售玩具获得利润w（元）