陕西省2016-2017学年中考模拟数学考试试卷（一）

试卷更新日期：2017-08-23 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣3的相反数是（）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、3 D、﹣3

查看试题解析
2.
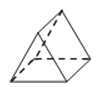
如图所示的几何体的左视图是（　　）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、a²•a³=a⁶ B、a⁶÷a³=a² C、4x²﹣3x²=1 D、（﹣2a²）³=﹣8a⁶

查看试题解析
4. 如图，直线a∥b，直线c分别与a、b相交于A、B两点，AC⊥AB于点A，交直线b于点C．已知∠1=42°，则∠2的度数是（）

A、38° B、42° C、48° D、58°

查看试题解析
5. 若正比例函数的图象经过点（﹣1，2），则这个图象必经过点（）

A、（1，2） B、（﹣1，﹣2） C、（2，﹣1） D、（1，﹣2）

查看试题解析
6. 一组数据：3，4，5，6，6，的平均数、众数、中位数分别是（）

A、4.8，6，6 B、5，5，5 C、4.8，6，5 D、5，6，6

查看试题解析
7. 如图，∠A=∠B=90°，AB=7，AD=2，BC=3，在边AB上取点P，使得△PAD与△PBC相似，则这样的P点共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，CD=2，则sin∠ECB为（）

A、 $\frac{3}{5}$ B、 $\frac{3 \sqrt{13}}{13}$ C、 $\frac{2}{3}$ D、 $\frac{2 \sqrt{13}}{13}$

查看试题解析
9. 如图，矩形ABCD中，AB=8，AD=6，将矩形ABCD绕点B按顺时针方向旋转后得到矩形A′BC′D′．若边A′B交线段CD于H，且BH=DH，则DH的值是（）

A、 $\frac{7}{4}$ B、 $8 - 2 \sqrt{3}$ C、 $\frac{25}{4}$ D、 $6 \sqrt{2}$

查看试题解析
10. 如图为二次函数y=ax²+bx+c（a≠0）的图象，则下列说法：
①a＞0 ②2a+b=0 ③a+b+c＞0 ④当﹣1＜x＜3时，y＞0
其中正确的个数为（）

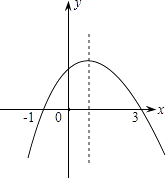A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 因式分解：（a+b）²﹣4b²= ．

查看试题解析
12. 请从以下两个小题中任选一个作答，若多选，则按第一题计分．
A．一个正n边形（n＞4）的内角和是外角和的3倍，则n=；
B．小明站在教学楼前50米处，测得教学楼顶部的仰角为20°，测角仪的高度为1.5米，则此教学楼的高度为米．（用科学计算器计算，结果精确到0.1米）

查看试题解析
13.
如图，矩形ABCD中，AD=3，∠CAB=30°，点P是线段AC上的动点，点Q是线段CD上的动点，则AQ+QP的最小值是．

查看试题解析
14. 如图，在第一象限内，点P（2，3），M（a，2）是双曲线y= $\frac{k}{x}$ （k≠0）上的两点，PA⊥x轴于点A，MB⊥x轴于点B，PA与OM交于点C，则△OAC的面积为．

查看试题解析

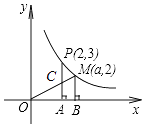
三、解答题

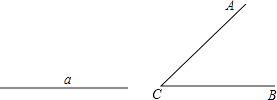
15. 计算：（ $\sqrt{3}$ ﹣2）⁰+（ $\frac{1}{3}$ ）^﹣1+4cos30°﹣| $\sqrt{3}$ ﹣ $\sqrt{27}$ |

查看试题解析
16. 先化简，再求值：（ $\frac{2}{a + 1}$ + $\frac{a + 2}{a^{2} - 1}$ ）÷ $\frac{a}{a - 1}$ ，其中a= $\sqrt{2}$ ﹣1．

查看试题解析
17. 已知：线段a及∠ACB．
求作：⊙O，使⊙O在∠ACB的内部，CO=a，且⊙O与∠ACB的两边分别相切．

查看试题解析
18. 某学校为了解七年级男生体质健康情况，随机抽取若干名男生进行测试，测试结果分为优秀、良好、合格、不合格四个等级，统计整理数据并绘制图1、图2两幅不完整的统计图，请根据图中信息回答下列问题：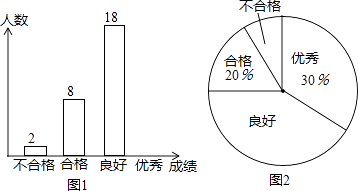

(1)、本次接收随机抽样调查的男生人数为人，扇形统计图中“良好”所对应的圆心角的度数为；

(2)、补全条形统计图中“优秀”的空缺部分；

(3)、若该校七年级共有男生480人，请估计全年级男生体质健康状况达到“良好”的人数．

查看试题解析
19. 如图，四边形ABCD中，E点在AD上，其中∠BAE=∠BCE=∠ACD=90°，且BC=CE，求证：△ABC≌△DEC．

查看试题解析
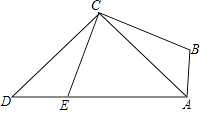20. 如图，一电线杆AB的影子分别落在了地上和墙上．同一时刻，小明竖起1米高的直杆MN，量得其影长MF为0.5米，量得电线杆AB落在地上的影子BD长3米，落在墙上的影子CD的高为2米．你能利用小明测量的数据算出电线杆AB的高吗？

查看试题解析
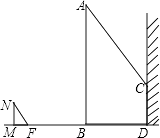21. 暑假期间，小刚一家乘车去离家380公里的某景区旅游，他们离家的距离y（km）与汽车行驶时间x（h）之间的函数图象如图所示．

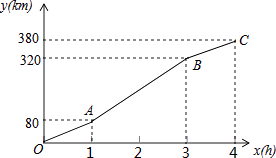(1)、从小刚家到该景区乘车一共用了多少时间？

(2)、求线段AB对应的函数解析式；

(3)、小刚一家出发2.5小时时离目的地多远？

查看试题解析
22. 如图，小华和小丽两人玩游戏，她们准备了A、B两个分别被平均分成三个、四个扇形的转盘．游戏规则：小华转动A盘、小丽转动B盘．转动过程中，指针保持不动，如果指针恰好指在分割线上，则重转一次，直到指针指向一个数字所在的区域为止．两个转盘停止后指针所指区域内的数字之和小于6，小华获胜．指针所指区域内的数字之和大于6，小丽获胜．

(1)、用树状图或列表法求小华、小丽获胜的概率；

(2)、这个游戏规则对双方公平吗？请判断并说明理由．

查看试题解析
23. 如图，C为以AB为直径的⊙O上一点，AD和过点C的切线互相垂直，垂足为点D．

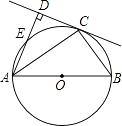(1)、求证：AC平分∠BAD；

(2)、若CD=3，AC=5，求⊙O的半径长．

查看试题解析
24. 如图，抛物线y= $\frac{1}{2}$ x²+bx﹣2与x轴交于A、B两点，与y轴交于C点，且A（一1，0）．

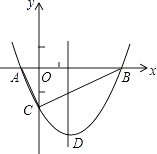(1)、求抛物线的解析式及顶点D的坐标；

(2)、判断△ABC的形状，证明你的结论；

(3)、点M是抛物线对称轴上的一个动点，当△ACM周长最小时，求点M的坐标及△ACM的最小周长．

查看试题解析
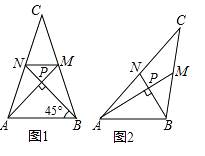
25. 爱好思考的小茜在探究两条直线的位置关系查阅资料时，发现了“中垂三角形”，即两条中线互相垂直的三角形称为“中垂三角形”．如图（1）、图（2）、图（3）中，AM、BN是△ABC的中线，AM⊥BN于点P，像△ABC这样的三角形均为“中垂三角形”．设BC=a，AC=b，AB=c．

(1)、
【特例探究】
如图1，当tan∠PAB=1，c=4 $\sqrt{2}$ 时，a= ， b=；
如图2，当∠PAB=30°，c=2时，a= ， b=；

(2)、
【归纳证明】
请你观察（1）中的计算结果，猜想a²、b²、c²三者之间的关系，用等式表示出来，并利用图3证明你的结论．

(3)、
【拓展证明】

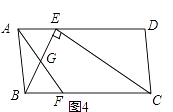
如图4，▱ABCD中，E、F分别是AD、BC的三等分点，且AD=3AE，BC=3BF，连接AF、BE、CE，且BE⊥CE于E，AF与BE相交点G，AD=3 $\sqrt{5}$ ，AB=3，求AF的长．

查看试题解析