山东省淄博市高青县2016-2017学年中考一模数学考试试卷
试卷更新日期:2017-08-23 类型:中考模拟
一、选择题
-
1. a6÷a3结果是( )A、a3 B、a2 C、a9 D、a﹣32. 在函数y= 中,自变量x的取值范围是( )A、x≤1 B、x≥1 C、x<1 D、x>13. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、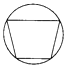 C、
C、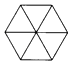 D、
D、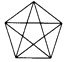 4. 在一个不透明的口袋中装有5张完全相同的卡片,卡片上面分别写有数字﹣2,﹣1,0,1,3,从中随机抽出一张卡片,卡片上面的数字是负数的概率为( )A、 B、 C、 D、5. 四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )A、AB=CD B、AD=BC C、AB=BC D、AC=BD6. 如图,▱ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE,∠E=36°,则∠ADC的度数是( )
4. 在一个不透明的口袋中装有5张完全相同的卡片,卡片上面分别写有数字﹣2,﹣1,0,1,3,从中随机抽出一张卡片,卡片上面的数字是负数的概率为( )A、 B、 C、 D、5. 四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )A、AB=CD B、AD=BC C、AB=BC D、AC=BD6. 如图,▱ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE,∠E=36°,则∠ADC的度数是( )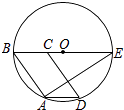 A、44° B、54° C、72° D、53°7. 若实数a,b(a≠b)分别满足方程a2﹣7a+2=0,b2﹣7b+2=0,则 的值为( )A、 B、 C、 或2 D、 或28. 三角形的两边长分别为2和6,第三边是方程x2﹣10x+21=0的解,则第三边的长为( )A、7 B、3 C、7或3 D、无法确定9. 若一次函数y=(m+1)x+m的图象过第一、三、四象限,则函数y=mx2﹣mx( )A、有最大值 B、有最大值﹣ C、有最小值 D、有最小值﹣10. 如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值为( )
A、44° B、54° C、72° D、53°7. 若实数a,b(a≠b)分别满足方程a2﹣7a+2=0,b2﹣7b+2=0,则 的值为( )A、 B、 C、 或2 D、 或28. 三角形的两边长分别为2和6,第三边是方程x2﹣10x+21=0的解,则第三边的长为( )A、7 B、3 C、7或3 D、无法确定9. 若一次函数y=(m+1)x+m的图象过第一、三、四象限,则函数y=mx2﹣mx( )A、有最大值 B、有最大值﹣ C、有最小值 D、有最小值﹣10. 如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值为( )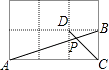 A、1 B、2 C、3 D、11. 如图,正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上,这四条直线中相邻两条之间的距离依次为h1、h2、h3 . 若h1=2,h2=1,则正方形ABCD的面积为( )
A、1 B、2 C、3 D、11. 如图,正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上,这四条直线中相邻两条之间的距离依次为h1、h2、h3 . 若h1=2,h2=1,则正方形ABCD的面积为( )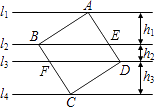 A、9 B、10 C、13 D、2512. 如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( )
A、9 B、10 C、13 D、2512. 如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( )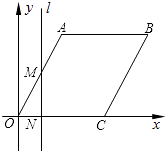 A、
A、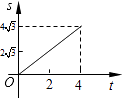 B、
B、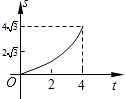 C、
C、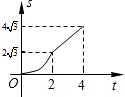 D、
D、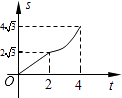
二、填空题
-
13. 已知一粒大米的质量约为0.000021千克,这个数用科学记数法表示为千克.14. 某校女子排球队队员的年龄分布如下表:
年龄
13
14
15
人数
4
7
4
则该校女子排球队队员的平均年龄是岁.
15. 如图,在菱形ABCD中,DE⊥AB,cosA= ,BE=2,则tan∠DBE= .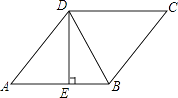 16. 如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y= 的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
16. 如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y= 的图象上,OA=1,OC=6,则正方形ADEF的边长为 .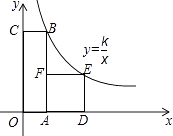 17. 如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1 , 此时AP1= ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+ ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+ ;…,按此规律继续旋转,直至得到点P2015为止.则AP2015= .
17. 如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1 , 此时AP1= ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+ ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+ ;…,按此规律继续旋转,直至得到点P2015为止.则AP2015= .
三、解答题
-
18. 解方程: .19. 如图,点C在线段AB上,△DAC和△DBE都是等边三角形.
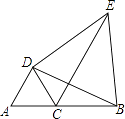 (1)、求证:△DAB≌△DCE;(2)、求证:DA∥EC.20. 如图,在平面直角坐标系中,反比例函数y= (x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).
(1)、求证:△DAB≌△DCE;(2)、求证:DA∥EC.20. 如图,在平面直角坐标系中,反比例函数y= (x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).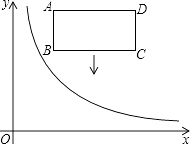 (1)、直接写出B、C、D三点的坐标;(2)、若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.21.
(1)、直接写出B、C、D三点的坐标;(2)、若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.21.“抢红包”是2015年春节十分火爆的一项网络活动,某企业有4000名职工,从中随机抽取350人,按年龄分布和对“抢红包”所持态度情况进行了调查,并将调查结果绘成了条形统计图和扇形统计图.
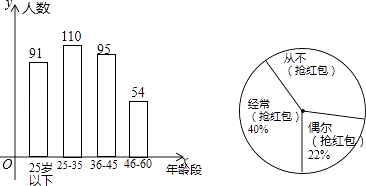 (1)、这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?(2)、如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?(3)、请估计该企业“从不(抢红包)”的人数是多少?22. 为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.(1)、求购进A、B两种纪念品每件各需多少元?(2)、若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?(3)、若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?23. 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足若 = ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
(1)、这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?(2)、如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?(3)、请估计该企业“从不(抢红包)”的人数是多少?22. 为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.(1)、求购进A、B两种纪念品每件各需多少元?(2)、若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?(3)、若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?23. 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足若 = ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.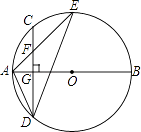 (1)、求证:△ADF∽△AED;(2)、求FG的长;(3)、求tan∠E的值.24. 如图,抛物线y=ax2+bx+c(a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
(1)、求证:△ADF∽△AED;(2)、求FG的长;(3)、求tan∠E的值.24. 如图,抛物线y=ax2+bx+c(a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.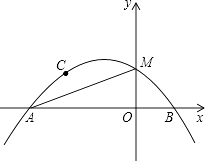 (1)、求抛物线的表达式;(2)、D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;(3)、抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A、N为顶点的三角形与△MAO相似(不包括全等)?若存在,求点P的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;(3)、抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A、N为顶点的三角形与△MAO相似(不包括全等)?若存在,求点P的坐标;若不存在,请说明理由.