山东省威海市环翠区火炬高技术产业开发区2016-2017学年中考模拟数学考试试卷
试卷更新日期:2017-08-23 类型:中考模拟
一、选择题
-
1. 关于 的叙述,错误的是( )A、 是无理数 B、面积为8的正方形边长是 C、 的立方根是2 D、在数轴上可以找到表示 的点2. 下列计算正确的是( )A、a6÷a3=a2 B、(ab3)3=ab6 C、(a+2)2=a2+4 D、x12÷x6=x63. 图中三视图对应的正三棱柱是( )
 A、
A、 B、
B、 C、
C、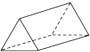 D、
D、 4. 不透明的袋子中装有形状、大小、质地完全相同的6个球,其中2个黑球、4个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是( )A、摸出的是3个白球 B、摸出的是3个黑球 C、摸出的是2个白球、1个黑球 D、摸出的是2个黑球、1个白球5. 如图,有一平行四边形ABCD与一正方形CEFG,其中E点在AD上.若∠ECD=35°,∠AEF=15°,则∠B的度数为何?( )
4. 不透明的袋子中装有形状、大小、质地完全相同的6个球,其中2个黑球、4个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是( )A、摸出的是3个白球 B、摸出的是3个黑球 C、摸出的是2个白球、1个黑球 D、摸出的是2个黑球、1个白球5. 如图,有一平行四边形ABCD与一正方形CEFG,其中E点在AD上.若∠ECD=35°,∠AEF=15°,则∠B的度数为何?( )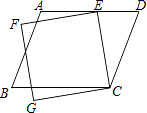 A、50 B、55 C、70 D、756. 已知一次函数y=kx+5和y=k′x+7,假设k>0且k′<0,则这两个一次函数的图象的交点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
A、50 B、55 C、70 D、756. 已知一次函数y=kx+5和y=k′x+7,假设k>0且k′<0,则这两个一次函数的图象的交点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( ) A、240米 B、160米 C、150米 D、140米8. 如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )
A、240米 B、160米 C、150米 D、140米8. 如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( ) A、7 B、8 C、7 D、79. 如图,AB为半圆O在直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:EC,⑤OD2=DE•CD,正确的有( )
A、7 B、8 C、7 D、79. 如图,AB为半圆O在直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:EC,⑤OD2=DE•CD,正确的有( ) A、2个 B、3个 C、4个 D、5个10. 以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )A、b≥ B、b≥1或b≤﹣1 C、b≥2 D、1≤b≤211. 如图,AB,CD是⊙O的两条互相垂直的直径,点O1 , O2 , O3 , O4分别是OA、OB、OC、OD的中点,若⊙O的半径为2,则阴影部分的面积为( )
A、2个 B、3个 C、4个 D、5个10. 以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )A、b≥ B、b≥1或b≤﹣1 C、b≥2 D、1≤b≤211. 如图,AB,CD是⊙O的两条互相垂直的直径,点O1 , O2 , O3 , O4分别是OA、OB、OC、OD的中点,若⊙O的半径为2,则阴影部分的面积为( ) A、8 B、4 C、4π+4 D、4π﹣4
A、8 B、4 C、4π+4 D、4π﹣4二、填空题
-
12. 分解因式:ab4﹣4ab3+4ab2= .13. 如图是一次射击训练中甲、乙两人的10次射击成绩的分布情况,则射击成绩的方差较小的是(填“甲”或“乙”).
 14. 若关于x的分式方程 =2﹣ 的解为正数,则满足条件的正整数m的值为 .15. 如图,直线l⊥x轴于点P,且与反比例函数y1= (x>0)及y2= (x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,则k1﹣k2= .
14. 若关于x的分式方程 =2﹣ 的解为正数,则满足条件的正整数m的值为 .15. 如图,直线l⊥x轴于点P,且与反比例函数y1= (x>0)及y2= (x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,则k1﹣k2= . 16. 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是 .
16. 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是 . 17. 如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1 , 它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2 , 交x轴于A2;将C2绕A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C2017 . 若点P是第2016段抛物线的顶点,则P点的坐标为 .
17. 如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1 , 它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2 , 交x轴于A2;将C2绕A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C2017 . 若点P是第2016段抛物线的顶点,则P点的坐标为 .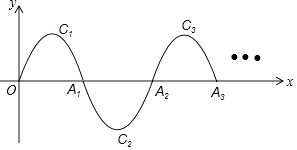
三、解答题
-
18. 关于x的两个不等式① <1与②1﹣3x>0(1)、若两个不等式的解集相同,求a的值;(2)、若不等式①的解都是②的解,求a的取值范围.19. 李师傅加工1个甲种零件和1个乙种零件的时间分别是固定的,现知道李师傅加工3个甲种零件和5个乙种零件共需55分钟;加工4个甲种零件和9个乙种零件共需85分钟,求李师傅加工2个甲种零件和4个乙种零件共需多少分钟.20. 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1: ,求大楼AB的高度是多少?(精确到0.1米,参考数据: ≈1.41, ≈1.73, ≈2.45)
 21. 在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图.
21. 在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图. (1)、调查发现评定等级为合格的男生有2人,女生有1人,则全班共有名学生.(2)、补全女生等级评定的折线统计图.(3)、根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率.22. 如图,CD为⊙O的直径,弦AB交CD于点E,连接BD、OB.
(1)、调查发现评定等级为合格的男生有2人,女生有1人,则全班共有名学生.(2)、补全女生等级评定的折线统计图.(3)、根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率.22. 如图,CD为⊙O的直径,弦AB交CD于点E,连接BD、OB. (1)、求证:△AEC∽△DEB;(2)、若CD⊥AB,AB=8,DE=2,求⊙O的半径.23. 如图1,菱形ABCD中,已知∠BAD=120°,∠EGF=60°,∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC,CD于点E,F.
(1)、求证:△AEC∽△DEB;(2)、若CD⊥AB,AB=8,DE=2,求⊙O的半径.23. 如图1,菱形ABCD中,已知∠BAD=120°,∠EGF=60°,∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC,CD于点E,F. (1)、 如图2,当顶点G运动到与点A重合时,求证:EC+CF=BC;
(1)、 如图2,当顶点G运动到与点A重合时,求证:EC+CF=BC; (2)、知识探究:①如图3,当顶点G运动到AC中点时,探究线段EC,CF与BC的数量关系;
(2)、知识探究:①如图3,当顶点G运动到AC中点时,探究线段EC,CF与BC的数量关系;②在顶点G的运动过程中,若 =t,请直接写出线段EC,CF与BC的数量关系(不需要写出证明过程);
 (3)、问题解决:如图4,已知菱形边长为8,BG=7,CF= ,当t>2时,求EC的长度.
(3)、问题解决:如图4,已知菱形边长为8,BG=7,CF= ,当t>2时,求EC的长度. 24. 综合与探究
24. 综合与探究如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(﹣2,0),(6,﹣8).
 (1)、求抛物线的函数表达式,并分别求出点B和点E的坐标;(2)、试探究抛物线上是否存在点F,使△FOE≌△FCE?若存在,请直接写出点F的坐标;若不存在,请说明理由;(3)、若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q,试探究:当m为何值时,△OPQ是等腰三角形.
(1)、求抛物线的函数表达式,并分别求出点B和点E的坐标;(2)、试探究抛物线上是否存在点F,使△FOE≌△FCE?若存在,请直接写出点F的坐标;若不存在,请说明理由;(3)、若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q,试探究:当m为何值时,△OPQ是等腰三角形.