辽宁省沈阳市于洪区2016-2017学年中考二模数学考试试卷
试卷更新日期：2017-08-23 类型：中考模拟
一、选择题
-
1. 图中的两个圆柱体底面半径相同而高度不同，关于这两个圆柱体的视图说法正确的是（ ）
A、主视图相同 B、俯视图相同 C、左视图相同 D、主视图、俯视图、左视图都相同2. 计算2x6÷x4的结果是（ ）A、x2 B、2x2 C、2x4 D、2x103. 如图，在△ABC中，∠B=40°，过点C作CD∥AB，∠ACD=65°，则∠ACB的度数为（ ）
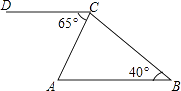A、60° B、65° C、70° D、75°4. 解分式方程 ，正确的结果是（ ）A、x=0 B、x=1 C、x=2 D、无解5. 已知实数a＜0，则下列事件中是必然事件的是（ ）A、a+3＜0 B、a﹣3＜0 C、3a＞0 D、a3＞06. 已知a﹣b=2，则代数式2a﹣2b﹣3的值是（ ）A、1 B、2 C、5 D、77. 下列说法不正确的是（ ）A、数据3、5、4、1、﹣2的中位数是3 B、数据1、1、0、2、4的平均数是2 C、在选举中，人们通常最关心是数据的众数 D、甲乙两人近5次数学考试平均分都是95分，方差分别是2.5和8.5，要选一人参加数学竞赛，选甲比较合适8. 如图，OP是∠AOB的平分线，点C，D分别在角的两边OA，OB上，添加下列条件，不能判定△POC≌△POD的选项是（ ）
A、PC⊥OA，PD⊥OB B、OC=OD C、∠OPC=∠OPD D、PC=PD9. 如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+3上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为（ ）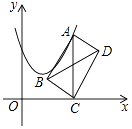
A、1 B、2 C、3 D、4二、填空题
-
10. 计算： = ．11. 一个多边形的内角和是720°，这个多边形的边数是 ．12. 图中的四边形均为矩形．根据图形，写出一个正确的等式： ．
13. 在平行四边形ABCD中，连接AC，按以下步骤作图，分别以A、C为圆心，以大于 AC的长为半径画弧，两弧分别相交于点M、N，作直线MN交CD于点E，交AB于点F．若AB=6，BC=4，则△ADE的周长为 ．
14. 函数yl=x（x≥0）， （x＞0）的图象如图所示，则结论：①两函数图象的交点A的坐标为（3，3）；
②当x＞3时，y2＞y1；
③当x=1时，BC=8；
④当x逐渐增大时，yl随着x的增大而增大，y2随着x的增大而减小．
其中正确结论的序号是
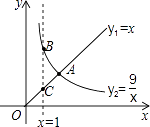15. 如图，在边长为2的菱形ABCD中，∠A=60°，点M是AD边的中点，连接MC，将菱形ABCD翻折，使点A落在线段CM上的点E处，折痕交AB于点N，则线段EC的长为 ．
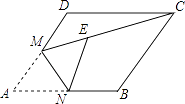16. 计算：4sin60°+|3﹣ |﹣（ ）﹣1+（π﹣2016）0 ．17. 在四张编号为A，B，C，D的卡片（除编号外，其余完全相同）的正面分别写上如图所示的正整数后，背面向上，洗匀放好．
(1)、从中随机抽取一张，若以卡片上的数字作为三角形的三边长，能构成三角形的概率为(2)、先从中随机抽取一张（不放回），再从剩下的卡片中随机抽取一张，请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率（满足a2+b2=c2的三个正整数a，b，c成为勾股数）
18. 如图，菱形ABCD的对角线AC，BD相交于点O，分别延长OA，OC到点E，F，使AE=CF，依次连接B，F，D，E各点．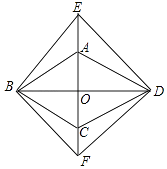
(1)、求证：△BAE≌△BCF；(2)、若∠ABC=40°，则当∠EBA=°时，四边形BFDE是正方形．19. 某校1000名学生参加了全区组织的“经典诵读”活动，该校随机选取部分学生，对他们在三、四两个月的诵读时间进行调查，下面是根据调查数据制作的统计图表的一部分．
根据以上信息，解答下列问题：
(1)、本次调查的学生数为人；(2)、四月日均诵读时间的统计表中的a值分别为；(3)、在被调查的学生中，四月份日人均诵读时间在1＜x≤1.5范围内的人数比三月份在此范围的人数多人；(4)、根据抽样调查结果，请你估计该校学生四月份人均诵读时间在1小时以上的人数．20. 如图，四边形APBC是圆内接四边形，∠APB=120°，PC平分∠APB，AP，CB的延长线相交于点D．
(1)、求证：△ABC是等边三角形；(2)、若∠PAC=90°，AB=2①求PD的长 ．
②图中弧BP和线段DP、BD组成的图形面积为（结果保留π）
21.某度假村依山而建，大门A处，有一斜坡AB，长度为13米，在坡顶B处测得度假村楼CF的楼顶C的仰角∠CBF=60∘，离B点8米远的E处有一花台，在E处仰望C的仰角∠CEF=73.5°，CF的延长线交校门处的水平面于D点，FD=5米．
(1)、求斜坡AB的坡度i．(2)、求DC的长．（参考数据：sin73.5°≈0.96，con73.5°≈0.28，tan73.5°≈3.4， ≈1.7）22. 如图（1），公路上有A、B、C三个车站，一辆汽车从A站以速度v1匀速驶向B站，到达B站后不停留，以速度v2匀速驶向C站，汽车行驶路程y（千米）与行驶时间x（小时）之间的函数图象如图（2）所示．
(1)、当汽车在A、B两站之间匀速行驶时，求y与x之间的函数关系式及自变量的取值范围；(2)、求出v2的值；(3)、若汽车在某一段路程内刚好用50分钟行驶了90千米，求这段路程开始时x的值．23.已知：如图①，在矩形ABCD中，AB=5，AD= ，AE⊥BD，垂足是E．点F是点E关于AB的对称点，连接AF、BF．
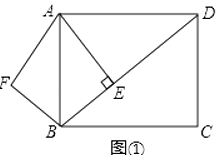(1)、求AE和BE的长；(2)、若将△ABF沿着射线BD方向平移，平移中的△ABF为△A1B1F1设平移的距离为m（平移距离指点B沿BD方向所经过的线段长度）．①当点F分别平移到线段AB上时，求出m的值
②当点F分别平移到线段AD上时，当直接写出相应的m的值．
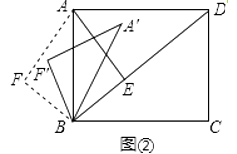
(3)、如图②，将△ABF绕点B顺时针旋转一个角α（0°＜α＜180°），记旋转中的△ABF为△A′BF′，在旋转过程中，设A′F′所在的直线与直线AE交于点O，当∠A′BD=∠FAB时，请直接写出OB的长．
24.如图1，在平面直角坐标系中，抛物线y=ax2+bx+3交x轴于A（﹣1，0）和B（5，0）两点，交y轴于点C，点D是线段OB上一动点，连接CD，将线段CD绕点D顺时针旋转90°得到线段DE，过点E作直线l⊥x轴于H，交抛物线于点M，过点C作CF⊥l于F．
(1)、求抛物线解析式；(2)、如图2，当点F恰好在抛物线上时（与点M重合）
①求点F的坐标；
②求线段OD的长；
③试探究在直线l上，是否存在点G，使∠EDG=45°？若存在，请直接写出点G的坐标；若不存在，请说明理由．
(3)、在点D的运动过程中，连接CM，若△COD∽△CFM，请直接写出线段OD的长．