辽宁省大连市2016-2017学年中考一模数学考试试卷

试卷更新日期：2017-08-23 类型：中考模拟

进入出卷网下载

一、选择题

1. 在实数﹣3，2，0，﹣1中，最小的数是（）

A、﹣3 B、2 C、0 D、﹣1

查看试题解析
2. 如图，点P在直线AB上，点C，D在直线AB的上方，且PC⊥PD，∠APC=28°，则∠BPD的度数为（）

A、28° B、60° C、62° D、152°

查看试题解析
3. 一个多边形的内角和是720°，这个多边形是（）

A、五边形 B、六边形 C、七边形 D、八边形

查看试题解析
4. 如图所示的几何体是由五个完全相同且棱长为1的正方体组成的，下列关于这个几何体的说法正确的是（）

A、主视图的面积为5 B、俯视图的面积为3 C、左视图的面积为3 D、三个视图的面积都为4

查看试题解析
5. 下列计算正确的是（）

A、a³﹣a²=a B、a²•a³=a⁶ C、（a﹣b）²=a²﹣b² D、（﹣a²）³=﹣a⁶

查看试题解析
6. 抛物线y=x²﹣4x﹣3的顶点坐标为（）

A、（2，﹣7） B、（2，7） C、（﹣2，﹣7） D、（﹣2，7）

查看试题解析
7. 同时掷两枚质地均匀的骰子，至少有一枚骰子的点数是2的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{5}{18}$ D、 $\frac{11}{36}$

查看试题解析
8. 如图，PA，PB是⊙O的切线，切点分别为A，B，点C在⊙O上，且 $\hat{A C B}$ 是优弧，则∠ACB等于（）

A、180°﹣2∠P B、180°﹣∠P C、90°﹣ $\frac{1}{2}$ ∠P D、∠P

查看试题解析

二、填空题

9. 分解因式：a﹣ab= ．

查看试题解析
10. 某校12名学生参加区级诗词大赛，他们得分情况如下表所示：
分数
87
88
90
93
97
人数
2
3
4
2
1
则这12名学生所得分数的众数是分．

查看试题解析
11. 如图，在△ABC中，∠ACB=90°，∠B=35°，CD是AB上的中线，则∠ADC=°．

查看试题解析
12. 不等式组 ${\begin{matrix} x - 1 > 2 x \\ 3 x - 2 > 2 (x - 2) \end{matrix}$ 的解集为．

查看试题解析
13. 如图，利用标杆BE测量建筑物的高度．若标杆BE的高为1.2m，测得AB=1.6m，BC=12.4m，则楼高CD为 m．

查看试题解析
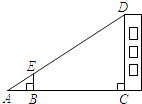14. 一艘轮船在静水中的最大航速为30km/h，它以最大航速沿顺流航行90km所用时间，与以最大航速逆流航行60km所用时间相等．设江水流速为vkm/h，则可列方程为．

查看试题解析
15. 当﹣1≤x≤1时，二次函数y=x²﹣3x+4的最小值为．

查看试题解析
16. 如图，在△ABC中，AB=AC，将△ABC绕顶点B顺时针旋转，得到△A′BC′．设∠A=α，当A′C′恰好经过顶点C时，∠A′BC=（用含α的式子表示）．

查看试题解析

三、解答题

17. 计算：（ $\sqrt{3}$ +1）（ $\sqrt{3}$ ﹣1）﹣ $\sqrt{18}$ + ${(\frac{1}{2})}^{- 3}$ ．

查看试题解析
18. 解方程： $\frac{3}{2} - \frac{1}{3 x - 1} = \frac{5}{6 x - 2}$ ．

查看试题解析
19. 如图，在▱ABCD中，点E在DA的延长线上，点F在BC的延长线上，且BE∥FD．求证：∠ABE=∠CDF．

查看试题解析
20. 某校未为了解学生每天参加体育锻炼的时间情况，随机选取该校的部分学生进行调查．以下是根据调查结果绘制的统计图表的一部分．
组别
A
B
C
D
E
时间t/min
t＜45
45≤t＜60
60≤t＜75
75≤t＜90
t≥90
人数
12
18
m
30
18
根据以上信息，解答下列问题：

(1)、被调查的学生中，每天参加体育锻炼的时间不少于90min的有人，这些学生数占被调查总人数的百分比为 %，每天参加体育锻炼的时间不足60min的有人；

(2)、被调查的学生总数为人，统计表中m的值为，统计图中n的值为，被调查学生每天参加体育锻炼时间的中位数落在组；

(3)、
该校共有960名学生，根据调查结果，估计该校每天参加体育锻炼的时间不少于60min的学生数．

查看试题解析
21. 有大小两种水桶，3个大桶与4个小桶一次最多可以装水220L，6个大桶与7个小桶一次最多可以装水415L.2个大桶与3个小桶一次最多可以装多少水？

查看试题解析
22. 如图，在平面直角坐标系xOy中，不经过原点的直线与双曲线y= $\frac{k}{x}$ 相交于点A（m，2），B（n，﹣1），其中m＞0，n＜0．

(1)、求m与n之间的数量关系；

(2)、若OA=OB，求该双曲线和直线的解析式．

查看试题解析
23. 如图1，⊙O是△ABC的外接圆，AP是⊙O的切线．已知AC=4，BC=5．

(1)、求证：∠PAC=∠ABC；

(2)、作∠BAC的平分线，与⊙O相交于点D，与BC相交于点E，连接并延长DC，与AP相交于点F（如图2），若AE=AC，求CF的长．

查看试题解析
24. 如图1，等边三角形ABC中，点D在AB上（点D与点A，B不重合），DE⊥BC，垂足为E，点P在BC上，且DP∥AC，△B′DE′与△BDE关于DP对称．设BE=x，△B′DE′与△ABC重叠部分的面积为S，S关于x的函数图象如图2所示（其中0＜x＜ $\frac{1}{2}$ ， $\frac{1}{2}$ ≤x＜m与m≤x＜n时，函数的解析式不同）．

(1)、填空：等边三角形ABC的边长为，图2中a的值为；

(2)、求S关于x的函数关系式，并直接写出x的取值范围．

查看试题解析
25.
如图1，在四边形ABCD中，AD∥BC，DB=DC=EC，∠A=2∠ADB，AD=m，AB=n．

(1)、在图1中找出与∠ABD相等的角，并加以证明；

(2)、求BE的长；

(3)、
将△ABD沿BD翻折，得到△A′BD．若点A′恰好落在EC上（如图2），求 $\frac{m}{n}$ 的值．

查看试题解析
26. 在平面直角坐标系xOy中，直线y=﹣ $\frac{5}{6}$ x+m经过点A（﹣2，n），B（1， $\frac{1}{2}$ ），抛物线y=x²﹣2tx+t²﹣1与x轴相交于点C，D．

(1)、求点A的坐标；

(2)、设点E的坐标为（ $\frac{5}{2}$ ，0），若点C，D都在线段OE上，求t的取值范围；

(3)、若该抛物线与线段AB有公共点，求t的取值范围．

查看试题解析

组别	A	B	C	D	E
时间t/min	t＜45	45≤t＜60	60≤t＜75	75≤t＜90	t≥90
人数	12	18	m	30	18

分数	87	88	90	93	97
人数	2	3	4	2	1