江西省吉安市2016-2017学年6月份中考模拟数学考试试卷-在线组卷题库

1. 在实数﹣3，0，5，3中，最小的实数是（）

A、﹣3 B、0 C、5 D、3

查看试题解析
2. 下列运算正确的是（）

A、π﹣3.14=0 B、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$ C、a³÷a=a² D、a•a=2a

查看试题解析
3. 数据2，0，17，6，17的中位数及众数分别是（）

A、0，6 B、2，6 C、6，17 D、2，17

查看试题解析
4. 将一包卷筒卫生纸按如图所示的方式摆放在水平桌面上，则它的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 如图，线段AB两个端点的坐标分别为A（6，6），B（8，2），以原点O为位似中心，在第一象限内将线段AB缩小为原来的 $\frac{1}{2}$ 后得到线段CD，则端点C的坐标为（）

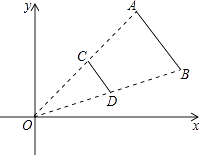A、（3，3） B、（4，3） C、（3，1） D、（4，1）

查看试题解析
6. 图中是有相同最小值的两条抛物线，则下列关系中正确的是（）

A、k＜n B、h=m C、k+n=0 D、h＜0，m＞0

查看试题解析

7. “一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行，中国预计为丝路基金新增资金1000亿人民币，1000亿用科学记数法表示为．

查看试题解析
8. 当整数a为时（只写一个），多项式x²+a能用平方差公式分解因式．

查看试题解析
9. 分式方程 $\frac{3}{2 x - 1}$ =1的解是．

查看试题解析
10. 一个多边形的内角和比外角和的3倍多180°，则它的边数是．

查看试题解析
11.
如图，在反比例函数图象中，△AOB是等边三角形，点A在双曲线的一支上，将△AOB绕点O顺时针旋转α（0°＜α＜180°），使点A仍在双曲线上，则α= ．

查看试题解析
12. 在Rt△ABC中，∠C=90°，∠A=30°，AB=6，点D，E分别是BC，AB上的动点，将△BDE沿直线DE翻折，点B的对应点B′恰好落在AC上，若△AEB′是等腰三角形，那么CB′的值是．

查看试题解析

13. 根据要求进行计算：

(1)、计算：| $\sqrt{2}$ |﹣（π﹣3）⁰+（ $\frac{1}{2}$ ）^﹣1﹣2cos45°

(2)、在矩形中，对角线AC，BD交于点O，AB=5cm，AC=13cm，求△ABO的周长．

查看试题解析
14. 解不等式组 ${\begin{matrix} 5 - x > 3 \\ \frac{x}{2} - \frac{2 x - 1}{3} - 1 \leq 0 \end{matrix}$ 并把解集在数轴上表示出来．

查看试题解析
15. 关于x的一元二次方程（a+c）x²+2bx+（a﹣c）=0，其中a、b、c分别为△ABC三边的长．

(1)、如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；

(2)、如果△ABC是等边三角形，试求这个一元二次方程的根．

查看试题解析
16. 等腰△ABC中，AB=AC，以AB为直径作圆交BC于点D，请仅用无刻度的直尺，根据下列条件分别在图1、图2中画一条弦，使这条弦的长度等于弦BD．（保留作图痕迹，不写作法）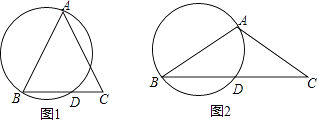

(1)、如图1，∠A＜90°；

(2)、如图2，∠A＞90°．

查看试题解析
17. 手机微信推出了红包游戏，它有多种玩法，其中一种为“拼手气红包”，用户设好总金额以及红包个数后，可以生成不等金额的红包，现有一用户发了三个“拼手气红包”，总金额为3元，随机被甲、乙、丙三人抢到．

(1)、下列事件中，确定事件是，
①丙抢到金额为1元的红包；
②乙抢不到金额为4元的红包
③甲、乙两人抢到的红包金额之和一定比丙抢到的红包金额多；

(2)、记金额最多、居中、最少的红包分别为A，B，C．求甲抢到红包A，乙抢到红包C的概率．

查看试题解析

18. 如图，已知△ABC内接于⊙O，AB是直径，OD∥AC，AD=OC．

(1)、当∠B=30°时，请判断四边形OCAD的形状，为什么？

(2)、当∠B等于多少度时，AD与⊙O相切？请说明理由．

查看试题解析
19. 吉安二中为了培养学生的兴趣，全面提高学生素质，从2013年开始在全市率先开设了拓展课，其中足球、茶艺、围棋、机器人四门课程是聘请校外专业老师授课，小颖协助老师随机抽取本校的部分学生，调查他们最喜欢的上述课程，并将调查结果绘制成如下两幅不完整的统计图，请你结合图中的信息解答下列问题：

(1)、求被调查的学生人数；

(2)、补全条形统计图；

(3)、已知该校有2160名学生，估计全校最喜欢足球的学生有多少人？

查看试题解析
20. 一种拉杆式旅行箱的示意图如图所示，箱体长AB=50cm，拉杆最大伸长距离BC=35cm，（点A、B、C在同一条直线上），在箱体的底端装有一圆形滚轮⊙A，⊙A与水平地面切于点D，AE∥DN，某一时刻，点B距离水平面38cm，点C距离水平面59cm．

(1)、求圆形滚轮的半径AD的长；

(2)、当人的手自然下垂拉旅行箱时，人感觉较为舒服，已知某人的手自然下垂在点C处且拉杆达到最大延伸距离时，点C距离水平地面73.5cm，求此时拉杆箱与水平面AE所成角∠CAE的大小（精确到1°，参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）．

查看试题解析

21.
如图，反比例函数y= $\frac{m}{x}$ （x＞0）的图象经过线段OA的端点A，O为原点，作AB⊥x轴于点B，点B的坐标为（2，0），tan∠AOB= $\frac{3}{2}$ ．

(1)、求m的值；

(2)、将线段AB沿x轴正方向平移到线段DC的位置，反比例函数y= $\frac{m}{x}$ （x＞0）的图象恰好经过DC的中点E，求直线AE的函数表达式；

(3)、若直线AE与x轴交于点M，与y轴交于点N，问线段AN与线段ME的大小关系如何？请说明理由．

查看试题解析
22.
如图，已知A（0，4），E（8，0），点P（a，0）是线段OE上的动点，点B为AP的中点，以BP为边向右边作正方形PBCD，过点B作BM⊥x轴于点M，过点D作DF⊥x轴于点F，连接DE．

(1)、判断DF，BM，MF之间的关系，并说明理由；

(2)、求点D的坐标（用含a的代数式表示）；

(3)、当点P在线段OE（点O，点E除外）上运动时，设△PDE的面积为S，写出S与a的函数关系式，当点P运动到何处时，△PDE的面积最大，最大是多少？

查看试题解析

23. 已知抛物线C：y₁=a（x﹣1）²+k₁（a≠0）交x轴于点M（﹣2，0）与点A₁（b₁ ， 0），抛物线C₂：y₂=a（x﹣ $\frac{1}{2}$ b₁）²+k₂交x轴于点M（﹣2，0）与点A₂（b₂ ， 0），抛物线C₃：y₃=a（x﹣ $\frac{1}{2}$ b₂）²+k₃交x轴于点M（﹣2，0）与点A₃（b₃ ， 0），…按此规律，
抛物线C_n：y_n=a（x﹣ $\frac{1}{2}$ b_n_﹣1）²+k_n交x轴于点M（﹣2，0）与点A_n（b_n ， 0），（其中n为正整数），我们把抛物线C₁ ， C₂ ， C₃…，C_n称为系数a的抛物线族．

(1)、试求出b₁的值；

(2)、线段A_n_﹣1A_n的长为多少；

(3)、探究如下问题：（用含a的代数式表示）
①抛物线y₃的顶点坐标为（，）；
②依此类推第n条抛物线y_n的顶点坐标为（，）；

(4)、抛物线C₁₀的顶点N，是否存在△MNA₁₀是等腰直角三角形的情况？若存在，求出a的值；若不存在，请说明理由．

查看试题解析

江西省吉安市2016-2017学年6月份中考模拟数学考试试卷

一、选择题

二、填空题

三、解答题

四、解答题

五、解答题

六、解答题