吉林省长春市绿园区2016-2017年中考二模数学考试试卷
试卷更新日期:2017-08-23 类型:中考模拟
一、选择题
-
1. 在数﹣3,﹣2,0,3中,大小在﹣1和2之间的数是( )A、﹣3 B、﹣2 C、0 D、32. 微信根据移动ID所带来的数据,发布了“微信用户春节迁徙数据报告”,该报告显示,2016年1月24日春运首日至2月4日期间,人口流入最多的省份约有3 130 000微信用户在春节期间返乡.3 130 000用科学记数法可表示为( )A、3.13×102 B、313×104 C、3.13×105 D、3.13×1063. 某同学画出了如图所示的几何体的三种视图,其中正确的是( )

A、①② B、①③ C、②③ D、②4. 不等式组 的解在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 5. 如图,已知直线a、b被直线c所截,a∥b,∠1=60°,则∠2的度数为( )
5. 如图,已知直线a、b被直线c所截,a∥b,∠1=60°,则∠2的度数为( ) A、150° B、120° C、60° D、30°6. 如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( )
A、150° B、120° C、60° D、30°6. 如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( ) A、30° B、45° C、60° D、75°7. 我省2013年的快递业务量为1.4亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展,2014年增速位居全国第一.若2015年的快递业务量达到4.5亿件,设2014年与2015年这两年的平均增长率为x,则下列方程正确的是( )A、1.4(1+x)=4.5 B、1.4(1+2x)=4.5 C、1.4(1+x)2=4.5 D、1.4(1+x)+1.4(1+x)2=4.58. 如图在平面直角坐标系中,抛物线y=(x﹣h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )
A、30° B、45° C、60° D、75°7. 我省2013年的快递业务量为1.4亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展,2014年增速位居全国第一.若2015年的快递业务量达到4.5亿件,设2014年与2015年这两年的平均增长率为x,则下列方程正确的是( )A、1.4(1+x)=4.5 B、1.4(1+2x)=4.5 C、1.4(1+x)2=4.5 D、1.4(1+x)+1.4(1+x)2=4.58. 如图在平面直角坐标系中,抛物线y=(x﹣h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )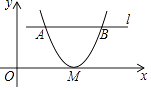 A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题
-
9. 分解因式:x2﹣3x=10. 若一元二次方程x2﹣2x+a=0有两个相等的实数根,则a的值是 .11. 如图,⊙O的半径为6,点A、B、C在⊙O上,且∠ACB=45°,则弦AB的长是 .
 12. 如图,▱ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.若△DEF的面积为1,则▱ABCD的面积为 .
12. 如图,▱ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.若△DEF的面积为1,则▱ABCD的面积为 . 13. 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ),则点C的坐标为 .
13. 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ),则点C的坐标为 . 14.
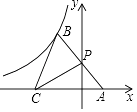
14.如图,双曲线y= 经过第二象限的点B,点P在y轴上,点A在x轴上,且点B与点A关于点P对称,若OC=2OA,△BCP的面积为4,则k的值是 .
三、解答题
-
15. 先化简,再求值: ÷ ﹣a,其中a=2.16. 某市今年中考理化实验操作考试,采用学生抽签方式决定自己的考试内容.规定每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学试验(用纸签D、E、F表示)中各抽取一个实验操作进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.用列表或画树状图的方法求小刚抽到物理实验B和化学实验F的概率.17. 如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.若点F是AE的中点,求证:BF⊥AF.
 18.
18.如图在数学活动课中,小敏为了测量小院内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为12m,则旗杆AB的高度是多少米?(参考值: ≈1.73, ≈1.41,结果精确到0.1米)
 19. 为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好的了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩,
19. 为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好的了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩,(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:

成绩/分
频数
频率
50≤x<60
10
0.05
60≤x<70
20
0.10
70≤x<80
30
b
80≤x<90
a
0.30
90≤x≤100
80
0.40
请根据所给信息,解答下列问题:
(1)、a= , b=;(2)、请补全频数分布直方图;(3)、若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等的人数.20. 小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(时)的函数图象如图所示. (1)、小张在路上停留小时,他从乙地返回时骑车的速度为千米/时;(2)、小王与小张同时出发,按相同路线匀速前往乙地,距甲地的路程y(千米)与时间x(时)的函数关系式为y=12x+10.小王与小张在途中共相遇几次?请你计算第一次相遇的时间.21. 数学李老师给学生出了这样一个问题:探究函数y= 图象与性质.小斌根据学习函数的经验,对函数y= 的图象与性质进行了探究.下面是小斌的探究过程,请补充完成:(1)、函数y= 的自变量x的取值范围是;(2)、根据下表所列出y与x对应值,在平面直角坐标系中描出各对以对应值为坐标的点,并画出该函数的图象;(3)、若直线y=x+b与函数y= 的图象无交点,请直接写出b的取值范围.
(1)、小张在路上停留小时,他从乙地返回时骑车的速度为千米/时;(2)、小王与小张同时出发,按相同路线匀速前往乙地,距甲地的路程y(千米)与时间x(时)的函数关系式为y=12x+10.小王与小张在途中共相遇几次?请你计算第一次相遇的时间.21. 数学李老师给学生出了这样一个问题:探究函数y= 图象与性质.小斌根据学习函数的经验,对函数y= 的图象与性质进行了探究.下面是小斌的探究过程,请补充完成:(1)、函数y= 的自变量x的取值范围是;(2)、根据下表所列出y与x对应值,在平面直角坐标系中描出各对以对应值为坐标的点,并画出该函数的图象;(3)、若直线y=x+b与函数y= 的图象无交点,请直接写出b的取值范围.x
…
﹣5
﹣4
﹣3
﹣2
﹣
﹣
0
1
2
3
4
5
…
y
…
2
3
﹣1
0
…
 22.
22.【感知】如图①,△ABC是等边三角形,点D、E分别在AB、BC边上,且AD=BE,易知:△ADC≌△BEA.
【探究】如图②,△ABC是等边三角形,点D、E分别在边BA、CB的延长线上,且AD=BE,△ADC与△BEA还全等吗?如果全等,请证明:如果不全等,请说明理由.
【拓展】如图③,在△ABC中,AB=AC,∠1=∠2,点D、E分别在BA、FB的延长线上,且AD=BE,若AF= CF=2BE,S△ABF=6,求S△BCD的大小.
 23.
23.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P从点A出发沿边AC向点C以每秒1个单位长度的速度运动,同时点Q从点C出发沿边CB向点B以每秒a个单位长度的速度运动,过点P作PD⊥BC,交AB于点D,连接PQ.当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
 (1)、当a=2时,解答下列问题:
(1)、当a=2时,解答下列问题:①QB= , PD= . (用含t的代数式分别表示)
(2)、当a为某个数值时,四边形PDBQ在某一时刻为菱形,求a的值及四边形PDBQ为菱形时t的值.(3)、当t=2时,在整个运动过程中,恰好存在线段PQ的中点M到△ABC三边距离相等,直接写出此刻a的值.24.如图①、图②、图③,在平面直角坐标系中,抛物线y=a(x﹣1)2+2﹣a与抛物线y=(a﹣2)(x﹣1)2+a分别与y轴交于点A、B,与对称轴x=1交于点C、D.作点A关于直线x=1的对称点A′,连接AA′,以AB、AA′为边作矩形ABEA′.设△ACD与矩形ABEA′重叠部分图形的面积为S.
 (1)、用含a的代数式表示线段CD的长.(2)、求AB=2AA′时的a值.(3)、当△ACD与矩形ABEA′重叠部分图形为三角形时,求S与a的函数关系式.(4)、作点D关于直线AA′的对称点D′,连接AD、A′D、A′D′、AD′,得到四边形ADA′D′.直接写出四边形ADA′D′与矩形ABEA′同时是正方形时的a值.
(1)、用含a的代数式表示线段CD的长.(2)、求AB=2AA′时的a值.(3)、当△ACD与矩形ABEA′重叠部分图形为三角形时,求S与a的函数关系式.(4)、作点D关于直线AA′的对称点D′,连接AD、A′D、A′D′、AD′,得到四边形ADA′D′.直接写出四边形ADA′D′与矩形ABEA′同时是正方形时的a值.