湖南省邵阳市邵东县2016-2017学年中考三模数学考试试卷

试卷更新日期：2017-08-23 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列运算，错误的是（）

A、（a²）³=a⁶ B、（x+y）²=x²+y² C、（ $\sqrt{5}$ ﹣1）⁰=1 D、61200=6.12×10⁴

查看试题解析
2. 下列命题中，不正确的是（）

A、一组邻边相等的矩形是正方形 B、等腰梯形的对角线相等 C、直角三角形斜边上的高等于斜边的一半 D、圆既是轴对称图形，又是中心对称图形

查看试题解析
3. 要使二次根式 $\sqrt{1 - x}$ 有意义，则x应满足（）

A、x≠1 B、x≥1 C、x≤1 D、x＜1

查看试题解析
4. 如图所示的图中，既是轴对称又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5.
如图，点C在直线AB上，∠ACD的度数比∠BCD的度数的3倍少20°，设∠ACD和∠BCD的度数分别为x、y，那么下面可以求出这两个角的度数的方程组是（）

A、 ${\begin{matrix} x + y = 180 \\ x = y - 20 \end{matrix}$ B、 ${\begin{matrix} x + y = 180 \\ x = 3 y - 20 \end{matrix}$ C、 ${\begin{matrix} x + y = 180 \\ x = 20 - 3 y \end{matrix}$ D、 ${\begin{matrix} x + y = 90 \\ x = 3 y - 20 \end{matrix}$

查看试题解析
6. 下列事件中，是必然事件的是（）

A、经过长期努力学习，你会成为科学家 B、抛出的篮球会下落 C、打开电视机，正在直播NBA D、从一批灯泡中任意拿一个灯泡，能正常发光

查看试题解析
7. 如图，在△ABC中，D、E分别是AC、BC上的点，若△ADB≌△EDB≌△EDC，则∠C的度数是（）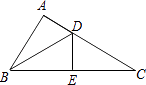

A、15° B、20° C、25° D、30°

查看试题解析
8. 如图，校园内有两棵树，相距8米，一棵树树高13米，另一棵树高7米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞（）

A、8米 B、9米 C、10米 D、11米

查看试题解析
9. 已知反比例函数 $y = \frac{k}{x}$ 的图象过一、三象限，则一次函数y=kx+k的图象经过（）

A、一、二、三象限 B、二、三、四象限 C、一、二、四象限 D、一、三、四象限

查看试题解析
10. 一次抽奖活动中，印发奖券1000张，其中一等奖20张，二等奖80张，三等奖200张，那么第一位抽奖者（仅买一张奖券）中奖的概率是（）

A、 $\frac{1}{50}$ B、 $\frac{2}{25}$ C、 $\frac{1}{5}$ D、 $\frac{3}{10}$

查看试题解析

二、填空题

11. 不等式 $\frac{x + 1}{3} < \frac{x - 1}{2}$ 的解集是．

查看试题解析
12. 如图，已知B、C在线段AD上，且MB=ND，∠MBA=∠NDC，请你添加一个条，使△ABM≌△CDN，你添加的条件是．

查看试题解析
13. 中华人民共和国国旗上的五角星的画法通常是先把圆五等分．然后连结五等分点而得（如图）．五角星的每一个角的度数是．

查看试题解析
14. 老师给出一个函数，甲、乙、丙各正确指出了这个函数的一个性质：甲：函数的图象是一条直线；乙：函数的图象经过点（1，1）；丙：y随x的增大而增大．
请你根据他们的叙述构造满足上述性质的一个函数：．

查看试题解析
15. 甲、乙两名同学在参加今年体育中考前各作了5次立定跳远测试，成绩如图所示，根据分析，你认为他们中成绩较为稳定的是．

查看试题解析

三、解答题

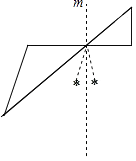
16. 计算：（3﹣π）⁰+ ${(\frac{1}{3})}^{- 1}$ ﹣2cos60°．

查看试题解析
17. 先化简，再求值： $\frac{a^{2} - 1}{a^{2} - 5 a + 6}$ ÷ $\frac{a^{2} + a - 2}{a - 3}$ ﹣ $\frac{a + 3}{a^{2} - 4}$ ，其中a=﹣3．

查看试题解析
18. 解方程： $\frac{2}{x - 1}$ + $\frac{2}{x + 2}$ =1．

查看试题解析
19. 尺规作图：把如图（实线部分）补成以虚线m为对称轴的轴对称图形，你会得到一只美丽蝴蝶的图案．（不用写作法，保留作图痕迹）．

查看试题解析
20. 如图，一位跳水运动员在进行某次10米跳台跳水训练时，测得身体（看成一点）在空中的运动路线是抛物线 $y = - \frac{25}{6} {(x - \frac{2}{5})}^{2} + \frac{2}{3}$ （图中标出的数据为已知条件）．

(1)、运动员在空中运动的最大高度离水面为多少米？

(2)、如果运动员在距水面高度为5米以前，必须完成规定的翻腾动作，并调整好入水姿势，否则就会出现失误．在这次试跳中，运动员在空中调整好入水姿势时，测得距池边的水平距离为 $3 \frac{3}{5}$ 米，问此次跳水会不会失误？并通过计算说明理由．

查看试题解析
21. 小红、小明、小芳在一起做游戏时，需要确定游戏的先后顺序，他们约定用“剪子、锤子、布”的方式确定，问在一个回合中三个人出手互不相同的情况有哪几种？在一个回合中三个人都出剪子的概率是多少？

查看试题解析

四、证明题

22.
如图，在四边形ABCD中，对角线AC与BD相交于P，请添加一个条件，使四边形ABCD的面积为：S_{四边形ABCD}= $\frac{1}{2}$ AC•BD，并说明理由．
解：添加的条件：
理由：

查看试题解析

五、应用题

23. 中国移动公司有神州行和大众卡两种业务｡神州行免月租，打市内电话0.39元/分；大众卡月租16元，打市内通话0.15元/分，用户可以任选其一：

(1)、请你分别写出两种业务中用户每月应支付的费用y（元）与打市内电话时间x（分）之间的函数关系式；

(2)、若某用户估计一个月内打市内电话的时间为70分钟，你认为选择哪种业务较为合算？

查看试题解析

六、图表阅读分析题

24. 某班50名同学进行数学测验，将所得成绩（得分取整数，最低分为50分）进行整理后分成五组，并绘成统计图（如图）．请结合统计图提供的信息，回答下列问题．

(1)、请将该统计图补充完整；

(2)、请你写出从图中获得的三个以上的信息；

(3)、老师随机抽取一份试卷来分析，抽取到哪一组学生试卷的可能性较大？

查看试题解析

七、综合探究题

25. 在如图所示的平面直角坐标系中，点C在y轴的正半轴上，四边形OABC为平行四边形，OA=2，∠AOC=60°，以OA为直径的⊙P经过点C，交BC于点D，DE⊥AB，交AB于E．

(1)、求点A和B的坐标；

(2)、求证：DE是⊙P的切线；

(3)、小明在解答本题时，发现连结DA并延长，交x轴于点N，则△AON是等腰三角形．由此，他断定：“x轴上一定存在除点N以外的点Q，使△AOQ也是等腰三角形，且点Q一定在⊙P外”．你同意他的看法吗？请充分说明理由．

查看试题解析