黑龙江省哈尔滨市平房区2016-2017学年中考三模数学考试试卷

试卷更新日期：2017-08-23 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列各数中最小的是（）

A、|﹣5| B、﹣2³ C、﹣（+3） D、 $\sqrt{16}$

查看试题解析
2. 下列运算，正确的是（　　）

A、a+a³=a⁴ B、a²•a³=a⁶ C、（a²）³=a⁶ D、a¹⁰÷a²=a⁵

查看试题解析
3. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 点（2，﹣4）在反比例函数y= $\frac{k}{x}$ 的图象上，下列各点中，不在此图象上的是（）

A、（﹣2，4） B、（1，﹣8） C、（﹣8，1） D、（1，8）

查看试题解析
5. 如图是由八个相同小正方体组合而成的几何体，则其左视图是（）

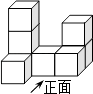A、 B、 C、 D、

查看试题解析
6. 在一个不透明的口袋中装有5个红球和若干个白球，每个球除颜色外都相同，随机摸出一个球是白球的概率为 $\frac{3}{4}$ ，则袋中的白球有（）个．

A、12 B、15 C、14 D、20

查看试题解析
7. 一件商品的进价为80元，七折售出仍可获利5%．若标价为x元，则可列方程为（）

A、80（1+5%）=0.7x B、80×0.7（1+5%）=x C、（1+5%）x=0.7x D、80×5%=0.7x

查看试题解析
8. 如图，电灯P在横杆AB的正上方，AB在灯光下的影长为CD，AB∥CD，AB=2m，CD=5m，点P到CD的距离是3m，则点P到AB的距离是（）

A、 $\frac{5}{6}$ m B、 $\frac{6}{7}$ m C、 $\frac{6}{5}$ m D、 $\frac{10}{3}$ m

查看试题解析
9. 如图，已知M是▱ABCD的AB边的中点，CM交BD于E，则图中阴影部分的面积与▱ABCD的面积之比是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{5}{12}$

查看试题解析
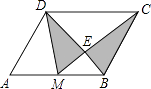10. 快车与慢车分别从相距420千米的甲乙两地同时相向出发，匀速而行，快车到达乙地后停留1小时，然后按原路原速返回，快车比慢车晚1小时到达甲地，快慢两车距各自出发地的路程y（千米）与所用的时间x（时）的关系如图所示，下列说法错误的是（）

A、快车返回的速度为140千米/时 B、慢车的速度为70千米/时 C、快慢两车出发4 $\frac{1}{2}$ 小时时两车相遇 D、出发 $\frac{14}{3}$ 小时时，快慢两车距各自出发地的路程相等

查看试题解析

二、填空题

11. 把数字315000用科学记数法表示为．

查看试题解析
12. 在函数y= $\frac{1}{2 - 3 x}$ 中，自变量x的取值范围是．

查看试题解析
13. 计算： $\sqrt{12} - \sqrt{27}$ = ．

查看试题解析
14. 因式分解：x³﹣9x= ．

查看试题解析
15. 圆心角为120°，弧长为12π的扇形半径为．

查看试题解析
16. 不等式组 ${\begin{matrix} 2 x + 1 > 0 \\ x - 3 \leq 0 \end{matrix}$ 的解集是．

查看试题解析
17. 如图所示，四边形ABCD中，∠B=90°，AB=2，CD=8，AC⊥CD，若sin∠ACB= $\frac{1}{3}$ ，则cos∠ADC= ．

查看试题解析
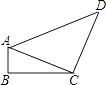18. 如图，AB是⊙O的直径，点D、C都在⊙O上，若∠ABC=2∠BDC，AB+BC=6，则弦AC= ．

查看试题解析
19. 在菱形ABCD中，对角线AC、BD相交于点O，点E在直线CD上，直线OE与边AD所在的直线交于点P．若菱形的边长为12，且EC=2DE，则AP= ．

查看试题解析
20. 如图，正方形ABCD的边长为1，点E、F分别在AC、DC上，若EC=BC，EF⊥BE，BF与EC交于点G，则 $\frac{E G}{C G}$ = ．

查看试题解析

三、解答题

21. 先化简，再求值： $\frac{x + 1}{x} \div (x - \frac{1 + x^{2}}{2 x})$ ，其中x=2sin45°+1．

查看试题解析
22.
如图，网格中每个小正方形的边长均为1，线段AB，线段CD的端点均在小正方形的顶点上．

(1)、在图中画以AB为斜边的等腰直角△ABE，顶点E在小正方形的顶点上；

(2)、在（1）的条件下，在图中以CD为边画直角△CDF，点F在小正方形的顶点上，使∠CDF=90°，且△CDF的面积为6，连接EF，直接写出EF的长．

查看试题解析
23. 为了增强中学生身体素质，某中学组织学生参加多种形式的运动．体育教师对九年一班同学参加锻炼的情况进行了统计（每人只能选其中一项），并绘制了下面的两个统计图，请根据图中提供的信息解答下列问题：

(1)、这次一共调查了多少名学生？

(2)、补全条形统计图，并求出扇形统计图中“足球”所在扇形的圆心角度数；

(3)、若该校有1800名学生，请估计该校喜欢乒乓球的学生约有多少人？

查看试题解析
24. 如图，在平行四边形ABCD中，延长BA至点E，使AE=AB，点F、P在边AD所在的直线上，EF∥CP．

(1)、求证：DF﹣DP=BC；

(2)、的条件下，若CD=15，EF=20，tan∠AFE= $\frac{3}{4}$ ，BC=14，求DF的长．

查看试题解析
25. 某商场购进甲、乙两种型号的小型家用电器，每个乙种型号电器的进价比每个甲种型号电器的进价的3倍少50元，用300元购进甲种电器的数量与用400元购进乙种型号电器的数量相同，请解答下列问题．

(1)、求甲、乙两种型号电器的进价；

(2)、若商场欲从厂家一次性购进甲、乙两种型号的电器共40个，且总费用不能超过1400元，则最多可以购进乙种型号电器多少个？

查看试题解析
26. 已知：△ABC内接于⊙O，点D在AB上，BD=CD，连接AO．

(1)、如图1，求证：∠OAC=∠OAB+∠ACD；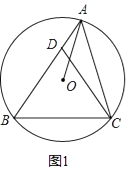

(2)、如图2，连接BO并延长交CD于点E，若BE⊥CD，求证：AC=BC；

(3)、如图3，在（2）的条件下，延长BE交⊙O于点F，连接AF、CF，若AF= $\frac{7}{2}$ ，AC=10，求△AFC的面积．

查看试题解析
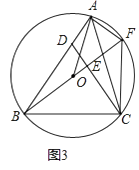27.
已知：如图，抛物线y=ax²+bx+6交x轴于A（﹣2，0），B（3，0）两点，交y轴于点C，

(1)、求a，b的值；

(2)、连接BC，点P为第一象限抛物线上一点，过点A作AD⊥x轴，过点P作PD⊥BC于交直线AD于点D，设点P的横坐标为t，AD长为d，求d与t的函数关系式（请求出自变量t的取值范围）；

(3)、在（2）的条件下，DP与BC交于点F，过点D作DE∥AB交BC于点E，点Q为直线DP上方抛物线上一点，连接AP、PC，若DP=CE，∠QPC=∠APD时，求点Q坐标．

查看试题解析