河北省唐山市路北区2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2020-03-13 类型:期中考试
一、单选题
-
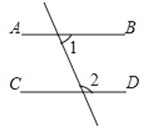
1. 的平方根是( )A、 B、 C、 D、2. 在平面直角坐标系中,点(-3,-2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列图形中,由∠1=∠2能得到AB∥CD的是( )A、
 B、
B、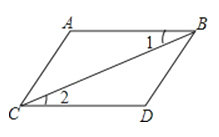 C、
C、 D、
D、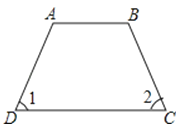 4. 下列命题中,是假命题的是( )A、两点之间,线段最短 B、同旁内角互补 C、直角的补角仍然是直角 D、对顶角相等5. 在 中,无理数的个数有( )A、1个 B、2个 C、3个 D、4个6. 下列说法正确是( )A、3是9的立方根 B、3是 的算术平方根 C、 的平方根是2 D、8的平方根是±47. 如图,点 在 的延长线上,下列条件中不能判定 的是( )
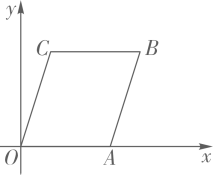
4. 下列命题中,是假命题的是( )A、两点之间,线段最短 B、同旁内角互补 C、直角的补角仍然是直角 D、对顶角相等5. 在 中,无理数的个数有( )A、1个 B、2个 C、3个 D、4个6. 下列说法正确是( )A、3是9的立方根 B、3是 的算术平方根 C、 的平方根是2 D、8的平方根是±47. 如图,点 在 的延长线上,下列条件中不能判定 的是( )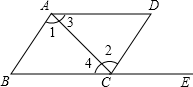 A、 B、 C、 D、8. 下列图形中,哪个可以通过图1平移得到( )。
A、 B、 C、 D、8. 下列图形中,哪个可以通过图1平移得到( )。 A、
A、 B、
B、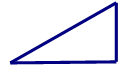 C、
C、 D、
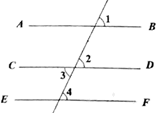
D、 9. 在平面直角坐标系中,A,B,C,D,M,N的位置如图所示,若点M的坐标为 ,N的坐标为 ,则在第二象限内的点是( )
9. 在平面直角坐标系中,A,B,C,D,M,N的位置如图所示,若点M的坐标为 ,N的坐标为 ,则在第二象限内的点是( )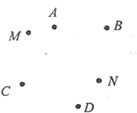 A、A点 B、B点 C、C点 D、D点10. 若点P(x,y)在第三象限,且点P到x轴的距离为3,到y轴的距离为2,则点P的坐标是( )
A、A点 B、B点 C、C点 D、D点10. 若点P(x,y)在第三象限,且点P到x轴的距离为3,到y轴的距离为2,则点P的坐标是( )
A、(-2,3) B、(-2,-3) C、(2,-3) D、(2,3)11. 如图,小手盖住的点的坐标可能为( )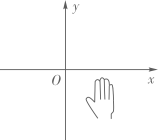 A、(-1,1) B、(-1,-1) C、(1,1) D、(1,-1)12. 若a2=9, =﹣2,则a+b=( )A、﹣5 B、﹣11 C、﹣5 或﹣11 D、±5或±1113. 实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简 的结果为( )
A、(-1,1) B、(-1,-1) C、(1,1) D、(1,-1)12. 若a2=9, =﹣2,则a+b=( )A、﹣5 B、﹣11 C、﹣5 或﹣11 D、±5或±1113. 实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简 的结果为( ) A、2a+b B、-2a+b C、b D、2a-b14. 如图,现将一块三角板的含有60°角的顶点放在直尺的一边上,若∠1=2∠2,那么∠1的度数为( )
A、2a+b B、-2a+b C、b D、2a-b14. 如图,现将一块三角板的含有60°角的顶点放在直尺的一边上,若∠1=2∠2,那么∠1的度数为( )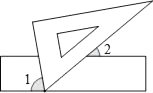 A、50° B、60° C、70° D、80°
A、50° B、60° C、70° D、80°二、填空题
-
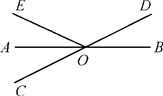
15. 7的平方根是 .16. 如图,直线AB , CD相交于点O , OA平分∠EOC , ∠EOD=120°,则∠BOD=°.
 17. 若x、y为实数,且满足 ,则xy的立方根为 .18. 如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=125°, 则∠DBC的度数为 .
17. 若x、y为实数,且满足 ,则xy的立方根为 .18. 如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=125°, 则∠DBC的度数为 .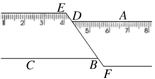
三、解答题
-
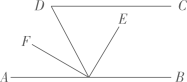
19. 计算:(1)、 ;(2)、20. 求x的值:(1)、 ;(2)、 .21. 已知:点 .试分别根据下列条件,求出P点的坐标.(1)、点P在y轴上;(2)、点P在x轴上;(3)、点P的纵坐标比横坐标大3;(4)、点P在过 点,且与x轴平行的直线上.22. 如图,已知 , ,试说明 .请将过程填写完整.
解:∵
又 ()
∴ .
∴∥()
又∵
∴
∴ ()
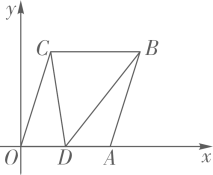
 23. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角空标系后,点A、B、C均在格点上.
23. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角空标系后,点A、B、C均在格点上.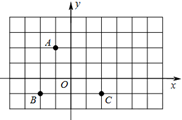 (1)、请直接写出点A,B,C的坐标.(2)、若平移线段AB,使B移动到C的位置,请在图中画出A移动后的位置D,依次连接B,C,D,A,并求出四边形ABCD的面积.
(1)、请直接写出点A,B,C的坐标.(2)、若平移线段AB,使B移动到C的位置,请在图中画出A移动后的位置D,依次连接B,C,D,A,并求出四边形ABCD的面积.