河北省石家庄市新乐市2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2020-03-13 类型:期中考试
一、单选题
-
1. 下列说法正确是( )A、相等的角是对顶角 B、一个角的补角必是钝角 C、同位角相等 D、一个角的补角比它的余角大90°2. 如图,直线a,b被直线c所截,∠1与∠2是( )
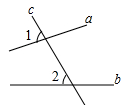 A、同位角 B、内错角 C、同旁内角 D、邻补角3. 《语文课程标准》规定:7﹣9年级学生,要求学会制订自己的阅读计划,广泛阅读各种类型的读物,课外阅读总量不少于260万字,每学年阅读两三部名著.那么260万用科学记数法可表示为( )A、26×105 B、2.6×102 C、2.6×106 D、260×1044. 在如图图形中,线段PQ能表示点P到直线L的距离的是( )A、
A、同位角 B、内错角 C、同旁内角 D、邻补角3. 《语文课程标准》规定:7﹣9年级学生,要求学会制订自己的阅读计划,广泛阅读各种类型的读物,课外阅读总量不少于260万字,每学年阅读两三部名著.那么260万用科学记数法可表示为( )A、26×105 B、2.6×102 C、2.6×106 D、260×1044. 在如图图形中,线段PQ能表示点P到直线L的距离的是( )A、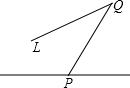 B、
B、 C、
C、 D、
D、 5. 已知am=2,an=3,则a3m+2n的值是( )A、6 B、24 C、36 D、726. 在下列图形中,由∠1=∠2一定能得到AB∥CD的是( )A、
5. 已知am=2,an=3,则a3m+2n的值是( )A、6 B、24 C、36 D、726. 在下列图形中,由∠1=∠2一定能得到AB∥CD的是( )A、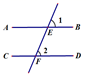 B、
B、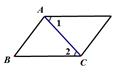 C、
C、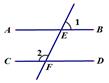 D、
D、 7. 已知 是方程kx+2y=﹣2的解,则k的值为( )A、﹣3 B、3 C、5 D、﹣58. 如果x2+kxy+36y2是完全平方式,则k的值是( )A、6 B、6或 C、12 D、12或9. 如图,AD是∠BAC的平分线,EF∥AC交AB于点E , 交AD于点F , 若∠1=30°,则∠AEF的度数为( )
7. 已知 是方程kx+2y=﹣2的解,则k的值为( )A、﹣3 B、3 C、5 D、﹣58. 如果x2+kxy+36y2是完全平方式,则k的值是( )A、6 B、6或 C、12 D、12或9. 如图,AD是∠BAC的平分线,EF∥AC交AB于点E , 交AD于点F , 若∠1=30°,则∠AEF的度数为( ) A、60° B、120° C、140° D、150°10. 小亮解方程组 的解为 ,由于不小心滴上了两滴墨水,刚好遮住了两个数●和★,则这两个数分别为( )A、4和6 B、6和4 C、2和8 D、8和﹣211. 如果方程组 的解与方程组 的解相同,则a+b的值为( )A、﹣1 B、1 C、2 D、012. 如图,长方形ABCD中,AB=8,第一次平移长方形ABCD沿AB的方向向右平移6个单位,得到长方形A1B1C1D1 , 第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移6个单位,得到长方形A2B2C2D2 , ……第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1的方向平移6个单位,得到长方形AnBn∁nDn(n>2),若ABn的长度为2018,则n的值为( )
A、60° B、120° C、140° D、150°10. 小亮解方程组 的解为 ,由于不小心滴上了两滴墨水,刚好遮住了两个数●和★,则这两个数分别为( )A、4和6 B、6和4 C、2和8 D、8和﹣211. 如果方程组 的解与方程组 的解相同,则a+b的值为( )A、﹣1 B、1 C、2 D、012. 如图,长方形ABCD中,AB=8,第一次平移长方形ABCD沿AB的方向向右平移6个单位,得到长方形A1B1C1D1 , 第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移6个单位,得到长方形A2B2C2D2 , ……第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1的方向平移6个单位,得到长方形AnBn∁nDn(n>2),若ABn的长度为2018,则n的值为( ) A、334 B、335 C、336 D、337
A、334 B、335 C、336 D、337二、填空题
-
13. 82018×(﹣0.125)2019= .14. 已知3x2m﹣2yn=1是关于x、y的二元一次方程,则mn= .15. 已知方程 ,用含有x的式子表示y为.16. 如果实数a,b满足a+b=6,ab=8,那么a2+b2=.17. 若(x+p)与(x+5)的乘积中不含x的一次项,则p= .18. 如图,把一个长方形纸片沿EF折叠后,点A,B分别落在A′,B′的位置,若∠A′FD=50°,则∠CEF等于.
 19. 已知三元一次方程组 ,则x+y+z= .20. 如图是我们常用的折叠式小刀,刀柄外形是一个矩形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成∠1与∠2,若∠1=75°,则∠2的度数为 .
19. 已知三元一次方程组 ,则x+y+z= .20. 如图是我们常用的折叠式小刀,刀柄外形是一个矩形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成∠1与∠2,若∠1=75°,则∠2的度数为 .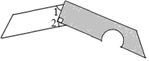
三、解答题
-
21. 先化简,再求值:(3x+2)(3x﹣2)﹣10x(x﹣1)+(x﹣1)2 , 其中x=﹣1.22. 若关于x、y的二元一次方程组 的解x、y互为相反数,求m的值.23. 图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图2拼成一个正方形.
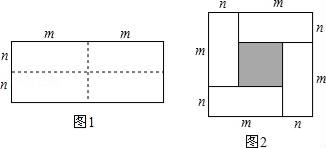 (1)、直接写出图2中的阴影部分面积;(2)、观察图2,请直接写出下列三个代数式(m+n)2 , (m﹣n)2 , mn之间的等量关系;(3)、根据(2)中的等量关系,解决如下问题:若p+q=9,pq=7,求(p﹣q)2的值.24. 如图,E为DF上的点,B为AC上的点,DF∥AC , ∠C=∠D , 求证:∠2=∠1.
(1)、直接写出图2中的阴影部分面积;(2)、观察图2,请直接写出下列三个代数式(m+n)2 , (m﹣n)2 , mn之间的等量关系;(3)、根据(2)中的等量关系,解决如下问题:若p+q=9,pq=7,求(p﹣q)2的值.24. 如图,E为DF上的点,B为AC上的点,DF∥AC , ∠C=∠D , 求证:∠2=∠1. 25. 我国古代数学著作《九章算术》中有这样一题,原文是:“今有大器五小器一容三斛,大器一小器五容二斛,问大小器各容几何.”意思是:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛(斛,是古代的一种容量单位),1个大桶加上5个小桶可以盛酒2斛.1个大桶、1个小桶分别可以盛酒多少斛?请解答.
25. 我国古代数学著作《九章算术》中有这样一题,原文是:“今有大器五小器一容三斛,大器一小器五容二斛,问大小器各容几何.”意思是:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛(斛,是古代的一种容量单位),1个大桶加上5个小桶可以盛酒2斛.1个大桶、1个小桶分别可以盛酒多少斛?请解答.
26.(1)、你能求出(a﹣1)(a99+a98+a97+…+a2+a+1)的值吗?遇到这样的问题,我们可以先从简单的情况入手,分别计算下列各式的值.(a﹣1)(a+1)=;
(a﹣1)(a2+a+1)=;
(a﹣1)(a3+a2+a+1)=;…
由此我们可以得到:(a﹣1)(a99+a98+…+a+1)= .
(2)、利用(1)的结论,完成下面的计算:2199+2198+2197+…+22+2+1.
27. 课题学习近平行线的“等角转化”功能.
阅读理解:
如图1,已知点A是BC外一点,连接AB,AC.
求∠BAC+∠B+∠C的度数.
(1)、阅读并补充下面推理过程解:过点A作ED∥BC,所以∠B=∠EAB,∠C= .
又因为∠EAB+∠BAC+∠DAC=180°,
所以∠B+∠BAC+∠C=180°
解题反思:
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决.
方法运用:
(2)、如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.(提示:过点C作CF∥AB)深化拓展:
(3)、如图3,已知AB∥CD,点C在点D的右侧,∠ADC=70°.点B在点A的左侧,∠ABC=60°,BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间,求∠BED的度数.