陕西省西安市师大附中2019-2020学年八年级下学期数学第一次月考试卷
试卷更新日期:2020-03-13 类型:月考试卷
一、选择题(共10小题,每小题3分,计30分。)
-
1. 下列说法正确的是( )A、无理数没有平方根 B、两个无理数的和还是无理数 C、无理数就是开方开不尽的数 D、任何实数都有立方根2. 估算 的值是( )A、在2和3之间 B、在3和4之间 C、在4和5之间 D、在5和6之间3. 一个数的平方根和立方根都等于它本身,则这个数是( )A、0 B、0、±1 C、0、1 D、14. 将一根长为25厘米的筷子至于底面直径为5厘米,高为12厘米的圆柱形水杯中,设筷子漏在杯子外的长为h厘米,则h的取值范围是( )A、12≤h≤13 B、11≤h≤12 C、11≤h≤13 D、10≤h≤125. 一幅三角板,如图所示叠放在一起,则图中∠a的度数是( )
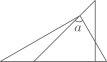 A、75° B、60° C、65° D、55°6. 如图,在长方形网格中每个小长方形网格的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形的面积为2,则满足条件的点C的个数是( )
A、75° B、60° C、65° D、55°6. 如图,在长方形网格中每个小长方形网格的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形的面积为2,则满足条件的点C的个数是( )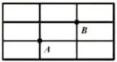 A、2 B、3 C、4 D、57. 已知点P(-2,3)与点Q关于x轴对称,则点Q的坐标是( )A、(-2,3) B、(-2,-3) C、(2,3) D、(2,-3)8. 如果代数式 有意义,那么直角坐标系中P(m,n)的位置是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 已知Rt△ABC中,∠C=90°,若a+b=10cm,c=8cm,则Rt△ABC的面积为( )A、9cm2 B、18cm2 C、24cm² D、36cm210. 如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△ADE以DE为折痕向右折叠,AE与BC交于点F,则EF的长为( )
A、2 B、3 C、4 D、57. 已知点P(-2,3)与点Q关于x轴对称,则点Q的坐标是( )A、(-2,3) B、(-2,-3) C、(2,3) D、(2,-3)8. 如果代数式 有意义,那么直角坐标系中P(m,n)的位置是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 已知Rt△ABC中,∠C=90°,若a+b=10cm,c=8cm,则Rt△ABC的面积为( )A、9cm2 B、18cm2 C、24cm² D、36cm210. 如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△ADE以DE为折痕向右折叠,AE与BC交于点F,则EF的长为( )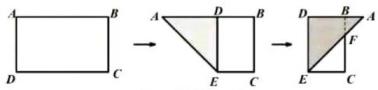 A、4 B、4 C、8 D、10
A、4 B、4 C、8 D、10二、填空题(共8小题,每小题3分,计24分)
-
11. 的立方根是2,则a= .12. 在△ABC中,∠C=90°,AB=5,则AB2+AC2+BC2= .13. 若一正数的两个平方根分别是2a-1与-a+2,则a= .14. 如图,已知正方形ABOC的顶点B(2,1),则顶点C的坐标为 .
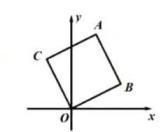 15. 若正方形ABCD的边长为4,E为BC上一点,BE=3,M为线段AB上一点,射线BM交正方形的一边于点F,且BF=AE,则BM的长为 .16. 设4- 的整数部分为a,小数部分为b,则a- = .17. 如图,长方体的底面边长分别为1厘米和4厘米,高为6厘米,如果用一根细线从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短需要厘米.(结果用含n的代数式表示)
15. 若正方形ABCD的边长为4,E为BC上一点,BE=3,M为线段AB上一点,射线BM交正方形的一边于点F,且BF=AE,则BM的长为 .16. 设4- 的整数部分为a,小数部分为b,则a- = .17. 如图,长方体的底面边长分别为1厘米和4厘米,高为6厘米,如果用一根细线从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短需要厘米.(结果用含n的代数式表示)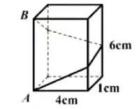 18. 如图,在平面直角坐标系中,规定把一个三角形先沿x轴翻折,再向右移动两个单位为一次变换,如图,已知等边三角形ABC经过连续2019次这样的变换得到三角形A'B'C', 则点A'的坐标是 .
18. 如图,在平面直角坐标系中,规定把一个三角形先沿x轴翻折,再向右移动两个单位为一次变换,如图,已知等边三角形ABC经过连续2019次这样的变换得到三角形A'B'C', 则点A'的坐标是 .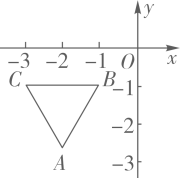
三、解答题(共7小题,计46分。)
-
19. 计算:(1)、(2)、(3)、(4)、20. 求下列各式中x的值.(1)、(3x+2)2=16(2)、 (2x-1)3=-421. 在数轴上找出 对应的点.22. △ABC在平面直角坐标系中的位置如图所示.
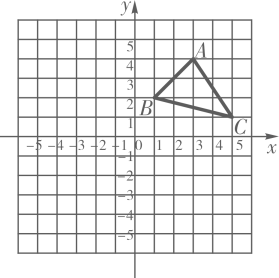 (1)、写出A、B、C三点的坐标;(2)、①若△ABC每个顶点的横坐标不变,纵坐标都乘以-1,请你在同一坐标系中描出对应的点A'、B'、C',并依次连接这三个点,所得的△A'B'C'与原△ABC有怎样的位置关系?
(1)、写出A、B、C三点的坐标;(2)、①若△ABC每个顶点的横坐标不变,纵坐标都乘以-1,请你在同一坐标系中描出对应的点A'、B'、C',并依次连接这三个点,所得的△A'B'C'与原△ABC有怎样的位置关系?
②在(①的基础上,纵坐标都不变,横坐标都乘以-1,请你在同一坐标系中描出对应的点A”、B”、C”,并依次连接这三个点,所得的△A”B”C”与原△ABC有怎样的位置关系?
23. 已知 =2,且|b-2c+1|+ =0,求 的值.24. 如图,△ABC中,CD是AB边上的高,CD=12,AC=20,BC=15,AE=AC,BF=BC,求EF的长. 25. 请阅读下列材料
25. 请阅读下列材料问题:如图1,点A、B在直线l的同侧,在直线l上找一点P,使得AP+BP的值最小,小明的思路是:如图2所示,先作点A关于直线l的对称点A',使点A'、B分别位于直线l的两侧,再连接A'B,根据“两点间线段最短”可知A'B与直线l的交点P即为所求.
 (1)、如图3,在图2的基础上,设AA'与直线l的交点为C,过点B作BD⊥l,垂足为D,若CP=1,AC=1,PD=2,求出AP+BP的值:(2)、将(1)中的条件“AC=1”去掉,换成“BD=4-AC”,其它条件不变,直接写出此时AP+BP的值:(3)、请结合图形,求 的最小值.
(1)、如图3,在图2的基础上,设AA'与直线l的交点为C,过点B作BD⊥l,垂足为D,若CP=1,AC=1,PD=2,求出AP+BP的值:(2)、将(1)中的条件“AC=1”去掉,换成“BD=4-AC”,其它条件不变,直接写出此时AP+BP的值:(3)、请结合图形,求 的最小值.