北京市海淀区2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2020-03-13 类型：期中考试

进入出卷网下载

一、单选题

1. 4的算术平方根是（）

A、16 B、±2 C、2 D、 $\sqrt{2}$

查看试题解析
2. 在平面直角坐标系中，点P(-3.2)在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 过点B画线段AC所在直线的垂线段，其中正确是（）

A、 B、 C、 D、

查看试题解析
4. 如图所示，AB∥CD ，若∠1＝144°，则∠2的度数是（）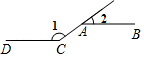

A、30° B、32° C、34° D、36°

查看试题解析
5. 在学习“用直尺和三角板画平行线”的时候，课本给出如图的画法，这种画平行线方法的依据是（）

A、内错角相等，两直线平行 B、同位角相等，两直线平行 C、两直线平行，内错角相等 D、两直线平行，同位角相等

查看试题解析
6. 如图，平移折线AEB ，得到折线CFD ，则平移过程中扫过的面积是（）

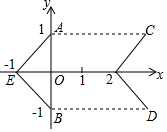A、4 B、5 C、6 D、7

查看试题解析
7. 小明和妈妈在家门口打车出行，借助某打车软件，他看到了当时附近的出租车分布情况．若以他现在的位置为原点，正东、正北分别为x轴、y轴正方向，图中点A的坐标为（1，0），那么离他最近的出租车所在位置的坐标大约是（）

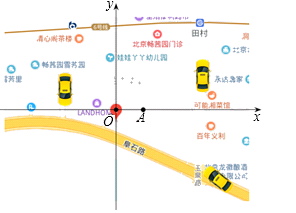A、（3.2，1.3） B、（﹣1.9，0.7） C、（0.8，﹣1.9） D、（3.8，﹣2.6）

查看试题解析
8. 我们知道“对于实数m ， n ， k ，若m＝n ， n＝k ，则m＝k”，即相等关系具有传递性．小敏由此进行联想，提出了下列命题：
①a ， b ， c是直线，若a∥b ， b∥c ，则a∥c ． ②a ， b ， c是直线，若a⊥b ， b⊥c ，则a⊥c ． ③若∠α与∠β互余，∠β与∠γ互余，则∠α与∠γ互余．其中正确命题是（）

A、① B、①② C、②③ D、①②③

查看试题解析

9. 根据表中的信息判断，下列语句中正确是（）

x	15	15.1	15.2	15.3	15.4	15.5	15.6	15.7	15.8	15.9	16
x²	225	228.01	231.04	234.09	237.16	240.25	243.36	246.49	249.64	252.81	256

A、

\sqrt{25.281}

＝1.59 B、235的算术平方根比15.3小 C、只有3个正整数n满足

15.5 < \sqrt{n} < 15.6

D、根据表中数据的变化趋势，可以推断出16.1²将比256增大3.19

查看试题解析

10. 如图所示是一个数值转换器，若输入某个正整数值x后，输出的y值为4，则输入的x值可能为（）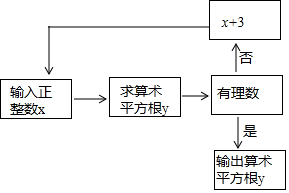

A、1 B、6 C、9 D、10

查看试题解析

二、解答题

11. 计算：

(1)、 $\sqrt{{(- 4)}^{2}} + {(\sqrt{\frac{1}{3}})}^{2} - \sqrt[3]{8}$ ；

(2)、 $\sqrt{2} (3 - \sqrt{2}) - 5 \sqrt{2}$ ．

查看试题解析
12. 求出下列等式中x的值：

(1)、12x²＝36；

(2)、 $\frac{x^{3}}{8} - 3 = \frac{3}{8}$ ．

查看试题解析
13. 下图是北京市三所大学位置的平面示意图，图中小方格都是边长为1个单位长度的正方形，若清华大学的坐标为（0，3），北京大学的坐标为（﹣3，2）．

(1)、请在图中画出平面直角坐标系，并写出北京语言大学的坐标；

(2)、若中国人民大学的坐标为（﹣3，﹣4），请在坐标系中标出中国人民大学的位置．

查看试题解析
14. 有一张面积为100cm²的正方形贺卡，另有一个长方形信封，长宽之比为5：3，面积为150cm² ，能将这张贺卡不折叠的放入此信封吗？请通过计算说明你的判断．

查看试题解析
15. 如图，点D ，点E分别在∠BAC的边AB ， AC上，点F在∠BAC内，若EF∥AB ， ∠BDF＝∠CEF ．
求证：DF∥AC ．

查看试题解析
16. 已知正实数x的平方根是m和m+b ．

(1)、当b＝8时，求m；

(2)、若m²x+（m+b）²x＝4，求x的值．

查看试题解析
17. 在平面直角坐标系xOy中，已知点A（a ， a），B（a ， a﹣3），其中a为整数．点C在线段AB上，且点C的横纵坐标均为整数．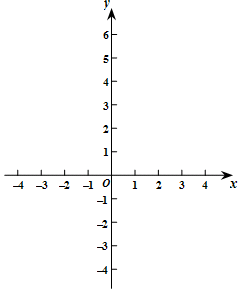

(1)、当a＝1时，画出线段AB；

(2)、若点C在x轴上，求出点C的坐标；

(3)、若点C纵坐标满足 $1 < y < \sqrt{5}$ ，直接写出a的所有可能取值：．

查看试题解析
18. 如图，已知AB∥CD ，点E是直线AB上一个定点，点F在直线CD上运动，设∠CFE＝α，在线段EF上取一点M ，射线EA上取一点N ，使得∠ANM＝160°．

(1)、当∠AEF＝ $\frac{a}{2}$ 时，α＝；

(2)、当MN⊥EF时，求α；

(3)、作∠CFE的角平分线FQ ，若FQ∥MN ，直接写出α的值：．

查看试题解析
19. 对于平面直角坐标系xOy中的不同两点A（x₁ ， y₁），B（x₂ ， y₂），给出如下定义：若x₁x₂＝1，y₁y₂＝1，则称点A ， B互为“倒数点”．例如，点A（ $\frac{1}{2}$ ，1），B（2，1）互为“倒数点”．

(1)、已知点A（1，3），则点A的倒数点B的坐标为；将线段AB水平向左平移2个单位得到线段A′B′，请判断线段A′B′上是否存在“倒数点”．（填“是”或“否”）；

(2)、如图所示，正方形CDEF中，点C坐标为（ $\frac{1}{2}$ ， $\frac{1}{2}$ ），点D坐标为（ $\frac{3}{2}$ ， $\frac{1}{2}$ ），请判断该正方形的边上是否存在“倒数点”，并说明理由；

(3)、已知一个正方形的边垂直于x轴或y轴，其中一个顶点为原点，若该正方形各边上不存在“倒数点”，请直接写出正方形面积的最大值：．

查看试题解析

三、填空题

20. 将点A（﹣1，4）向上平移三个单位，得到点A′，则A′的坐标为．

查看试题解析
21. 如图，数轴上点A ， B对应的数分别为﹣1，2，点C在线段AB上运动．请你写出点C可能对应的一个无理数．

查看试题解析
22. 如图，直线a ， b相交，若∠1与∠2互余，则∠3＝．

查看试题解析
23. 依据图中呈现的运算关系，可知a＝， b＝．

查看试题解析
24. 平面直角坐标系xOy中，已知线段AB与x轴平行，且AB＝5，若点A的坐标为（3，2），则点B的坐标是．

查看试题解析
25. 一副直角三角板如图放置，其中∠C＝∠DFE＝90°，∠A＝45°，∠E＝60°，点D在斜边AB上．现将三角板DEF绕着点D顺时针旋转，当DF第一次与BC平行时，∠BDE的度数是．

查看试题解析
26. 如图，电子宠物P在圆上运动，点O处设置有一个信号转换器，将宠物P的位置信号沿着垂直于线段OP的方向OQ传送，被信号接收板l接收．若传送距离越近，接收到的信号越强，则当P点运动到图中号点的位置时，接收到的信号最强（填序号①，②，③或④）．

查看试题解析
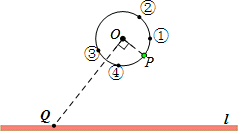27. 若两个图形有公共点，则称这两个图形相交，否则称它们不相交．回答下列问题：

(1)、如图1，直线PA ， PB和线段AB将平面分成五个区域（不包含边界），当点Q落在区域时，线段PQ与AB相交（直接填写区域序号）；

(2)、在设计印刷线路板时，常常会利用折线连接元件，要求所有连线不能相交．如图2，如果沿着图中的格线连接印有相同字母的元件，那么一共有种连线方案．

查看试题解析