河南省2016-2017学年中考原创押题数学考试试卷（三）

试卷更新日期：2017-08-22 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣5的相反数是（）

A、﹣5 B、5 C、﹣ $\frac{1}{5}$ D、 $\frac{1}{5}$

查看试题解析
2. 2016年10月17日神舟十一号飞船在酒泉发射中心成功发射，神舟十一号飞船是我国“神舟”系列飞船之一，每小时飞行约28000公里，将28000用科学记数法表示应为（）

A、2.8×10² B、2.8×10³ C、2.8×10⁴ D、2.8×10⁵

查看试题解析
3. 几个棱长为1的正方体组成的几何体的三视图如图所示，则这个几何体的体积是（）

A、4 B、5 C、6 D、7

查看试题解析
4. 实数a、b在数轴上的对应点的位置如图所示，则正确的结论是（）

A、a＜﹣b B、a＜﹣3 C、a＞﹣b D、a＞﹣2

查看试题解析
5. 如图，点A和点B都在反比例函数y= $\frac{4}{x}$ 的图象上，且线段AB过原点，过点A作x轴的垂线段，垂足为C，P是线段OB上的动点，连接CP．设△ACP的面积为S，则下列说法正确的是（）

A、S＞2 B、S＞4 C、2＜S＜4 D、2≤S≤4

查看试题解析
6. 在数轴上任取一个比﹣5大比7小的实数a对应的点，则取到的点对应的实数a满足|a|＞2的概率为（　　）

A、 $\frac{2}{7}$ B、 $\frac{1}{3}$ C、 $\frac{6}{11}$ D、 $\frac{2}{3}$

查看试题解析
7. 下列调查中，最适宜采用普查方式的是（）

A、对量子科学通信卫星上某种零部件的调查 B、对我国初中学生视力状况的调查 C、对一批节能灯管使用寿命的调查 D、对“最强大脑”节目收视率的调查

查看试题解析
8. 已知正比例函数y=ax（a≠0）与反比例函数y= $\frac{k}{x}$ （k≠0）图象的一个交点坐标为（﹣1，﹣1），则另一个交点坐标是（）

A、（1，﹣1） B、（1，1） C、（﹣1，1） D、（0，1）

查看试题解析
9. 如图，将矩形纸片ABCD折叠，使点B与点D重合，折痕为MN，若AB=2，BC=4，那么线段MN的长为（）

A、 $\frac{2 \sqrt{5}}{5}$ B、 $\sqrt{5}$ C、 $\frac{4 \sqrt{5}}{5}$ D、2 $\sqrt{5}$

查看试题解析
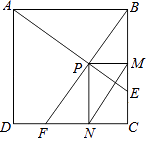
10.
如图，在边长为1的正方形ABCD中，动点F，E分别以相同的速度从D，C两点同时出发向C和B运动（任何一个点到达即停止），过点P作PM∥CD交BC于M点，PN∥BC交CD于N点，连接MN，在运动过程中，则下列结论：
①△ABE≌△BCF；②AE=BF；③AE⊥BF；④CF²=PE•BF；⑤线段MN的最小值为 $\frac{\sqrt{5} - 1}{2}$ ．
其中正确的结论有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 分解因式：3x²﹣6xy+3y²= ．

查看试题解析
12. 如图，等腰三角形ABC中，已知AB=AC，∠A=30°，AB的垂直平分线交AC于D，则∠CBD的度数为°．

查看试题解析
13. 若关于x的一元二次方程x²+3x+k=0有两个不相等的实数根，则k的取值范围是．

查看试题解析
14. 如图，将△ABC绕点C旋转60°得到△A′B′C′，已知AC=6，BC=4，则线段AB扫过图形（阴影部分）的面积为．（结果保留π）

查看试题解析
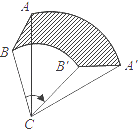15. 如图，在△ABC中，AB=BC=4，AO=BO，P是射线CO上的一个动点，∠AOC=60°，则当△PAB为直角三角形时，AP的长为．

查看试题解析

三、解答题

16. 先化简，再求值： $\frac{b^{2} - a^{2}}{a^{2} - a b} \div (a + \frac{2 a b + b^{2}}{a}) \cdot (\frac{1}{a} + \frac{1}{b})$ ，其中a= $\sqrt{2} + \sqrt{3}$ ，b= $\sqrt{2} - \sqrt{3}$ ．

查看试题解析
17. 某运动品牌店对第一季度A、B两款运动鞋的销售情况进行统计．两款运动鞋的销售量及总销售额如图所示：

(1)、一月份B款运动鞋的销售量是A款的 $\frac{4}{5}$ ，则一月份B款运动鞋销售了多少双？

(2)、第一节度这两款运动鞋的销售单价保持不变，求三月份的总销售额（销售额=销售单价×销售量）；

(3)、综合第一季度的销售情况，请你对这两款运动鞋的进货、销售等方面提出一条建议．

查看试题解析
18. 如图，△ABC中，AB=AC，以AB为直径作⊙O，交BC于点D，交CA的延长线于点E，连接AD、DE．

(1)、求证：D是BC的中点；

(2)、若DE=3，BD﹣AD=2，求⊙O的半径；

(3)、在（2）的条件下，求弦AE的长．

查看试题解析
19.
如图，为了开发利用海洋资源，某勘测飞机预测量一岛屿两端A、B的距离，飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°，然后沿着平行于AB的方向水平飞行了500米，在点D测得端点B的俯角为45°，求岛屿两端A、B的距离（结果精确到0.1米，参考数据： $\sqrt{3} \approx 1.73 ， \sqrt{2} \approx 1.41$ ）

查看试题解析
20. 为更新果树品种，某果园计划新购进A、B两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中A种苗的单价为7元/棵，购买B种苗所需费用y（元）与购买数量x（棵）之间存在如图所示的函数关系．

(1)、求y与x的函数关系式；

(2)、若在购买计划中，B种苗的数量不超过35棵，但不少于A种苗的数量，请设计购买方案，使总费用最低，并求出最低费用．

查看试题解析
21.
如图，一次函数y=﹣ $\frac{\sqrt{3}}{3}$ x+1的图象与x轴、y轴分别交于点A、B，以线段AB为边在第一象限内作等边△ABC．

(1)、求△ABC的面积；

(2)、如果在第二象限内有一点P（a， $\frac{1}{2}$ ），请用含a的式子表示四边形ABPO的面积，并求出当△ABP的面积与△ABC的面积相等时a的值．

查看试题解析
22. 问题提出

(1)、
如图①，已知△ABC，请画出△ABC关于直线AC对称的三角形．

(2)、
问题探究
如图②，在矩形ABCD中，AB=4，AD=6，AE=4，AF=2，是否在边BC、CD上分别存在点G、H，使得四边形EFGH的周长最小？若存在，求出它周长的最小值；若不存在，请说明理由．

(3)、
如图③，有一矩形板材ABCD，AB=3米，AD=6米，现想从此板材中裁出一个面积尽可能大的四边形EFGH部件，使∠EFG=90°，EF=FG= $\sqrt{5}$ 米，∠EHG=45°，经研究，只有当点E、F、G分别在边AD、AB、BC上，且AF＜BF，并满足点H在矩形ABCD内部或边上时，才有可能裁出符合要求的部件，试问能否裁得符合要求的面积尽可能大的四边形EFGH部件？若能，求出裁得的四边形EFGH部件的面积；若不能，请说明理由．

查看试题解析
23.
如图，在矩形OABC中，AO=10，AB=8，沿直线CD折叠矩形OABC的一边BC，使点B落在OA边上的点E处．分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系，抛物线y=ax²+bx+c经过O，D，C三点．

(1)、求AD的长及抛物线的解析式；

(2)、一动点P从点E出发，沿EC以每秒2个单位长的速度向点C运动，同时动点Q从点C出发，沿CO以每秒1个单位长的速度向点O运动，当点P运动到点C时，两点同时停止运动．设运动时间为t秒，当t为何值时，以P、Q、C为顶点的三角形与△ADE相似？

(3)、点N在抛物线对称轴上，点M在抛物线上，是否存在这样的点M与点N，使以M，N，C，E为顶点的四边形是平行四边形？若存在，请直接写出点M与点N的坐标（不写求解过程）；若不存在，请说明理由．

查看试题解析