河南省信阳市罗山县2016-2017学年中考数学信息试卷
试卷更新日期:2017-08-22 类型:中考模拟
一、选择题
-
1. ﹣7的绝对值是( )A、7 B、﹣7 C、 D、﹣2.
有一正方体,六个面上分别写有数字1,2,3,4,5,6,有三个人从不同的角度观察的结果如图.如果记6的对面的数字为a,2的对面的数字为b,那么a+b的值为( )
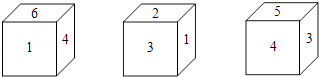 A、3 B、7 C、8 D、113. PM2.5“超细灰尘”主要来自机动车尾气尘、燃油尘、硫酸盐、餐饮油烟尘、建筑水泥尘、煤烟尘和硝酸盐等,它是雾霾有害细颗粒的重要组成部分.而PM2.5可直接被人体吸入肺部,由于其穿透力强,因此对人类的危害非常大,PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为( )A、0.25×10﹣5 B、0.25×10﹣6 C、2.5×10﹣5 D、2.5×10﹣64. 在平面直角坐标系中,若将抛物线y=2x2﹣4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是( )A、(﹣2,3) B、(﹣1,4) C、(1,4) D、(4,3)5. 下列说法正确的是( )A、一个游戏的中奖概率是 , 则做100次这样的游戏一定会中奖 B、为了解全国中学生的心理健康情况,应该采用普查的方式 C、一组数据 8,8,7,10,6,8,9 的众数和中位数都是8 D、若甲组数据的方差s2=0.01,乙组数据的方差s2=0.1,则乙组数据比甲组数据稳定6. 如图,在△ABC中,分别以点A和点B为圆心,以大于 AB的长为半径画弧,两弧相交于点M、N,作直线MN,交BC于点D,若△ADC的周长为10,AB=6,则△ABC的周长为( )
A、3 B、7 C、8 D、113. PM2.5“超细灰尘”主要来自机动车尾气尘、燃油尘、硫酸盐、餐饮油烟尘、建筑水泥尘、煤烟尘和硝酸盐等,它是雾霾有害细颗粒的重要组成部分.而PM2.5可直接被人体吸入肺部,由于其穿透力强,因此对人类的危害非常大,PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为( )A、0.25×10﹣5 B、0.25×10﹣6 C、2.5×10﹣5 D、2.5×10﹣64. 在平面直角坐标系中,若将抛物线y=2x2﹣4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是( )A、(﹣2,3) B、(﹣1,4) C、(1,4) D、(4,3)5. 下列说法正确的是( )A、一个游戏的中奖概率是 , 则做100次这样的游戏一定会中奖 B、为了解全国中学生的心理健康情况,应该采用普查的方式 C、一组数据 8,8,7,10,6,8,9 的众数和中位数都是8 D、若甲组数据的方差s2=0.01,乙组数据的方差s2=0.1,则乙组数据比甲组数据稳定6. 如图,在△ABC中,分别以点A和点B为圆心,以大于 AB的长为半径画弧,两弧相交于点M、N,作直线MN,交BC于点D,若△ADC的周长为10,AB=6,则△ABC的周长为( ) A、6 B、12 C、16 D、207. 不等式组 的解集在数轴上表示为( )A、
A、6 B、12 C、16 D、207. 不等式组 的解集在数轴上表示为( )A、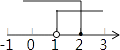 B、
B、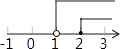 C、
C、 D、
D、 8. 绿苑小区在规划设计时,准备在两幢楼房之间,设置一块面积为900平方米的矩形绿地,并且长比宽多10米.设绿地的宽为x米,根据题意,可列方程为( )A、x(x﹣10)=900 B、x(x+10)=900 C、10(x+10)=900 D、2[x+(x+10)]=9009. 如图,在矩形ABCD中,由8个面积均为1的小正方形组成的L型模板如图放置,则矩形ABCD的周长为( )
8. 绿苑小区在规划设计时,准备在两幢楼房之间,设置一块面积为900平方米的矩形绿地,并且长比宽多10米.设绿地的宽为x米,根据题意,可列方程为( )A、x(x﹣10)=900 B、x(x+10)=900 C、10(x+10)=900 D、2[x+(x+10)]=9009. 如图,在矩形ABCD中,由8个面积均为1的小正方形组成的L型模板如图放置,则矩形ABCD的周长为( ) A、 B、 C、 D、10. 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中:①ac>0;②a+b+c<0;③4a﹣2b+c<0;④2a+b<0;⑤4ac﹣b2<4a;⑥a+b>0中,其中正确的个数为( )
A、 B、 C、 D、10. 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中:①ac>0;②a+b+c<0;③4a﹣2b+c<0;④2a+b<0;⑤4ac﹣b2<4a;⑥a+b>0中,其中正确的个数为( )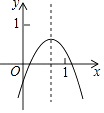 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
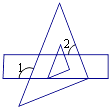
11. 计算 ﹣|﹣2|= .12. 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=115°,那么∠2是度.
 13. 如图所示,在△ABC中,AC=BC=4,∠C=90°,O是AB的中点,⊙O与AC、BC分别相切于点D、E,点F是⊙O与AB的一个交点,连接DF并延长交CB的延长线于点G,则BG的长是 .
13. 如图所示,在△ABC中,AC=BC=4,∠C=90°,O是AB的中点,⊙O与AC、BC分别相切于点D、E,点F是⊙O与AB的一个交点,连接DF并延长交CB的延长线于点G,则BG的长是 .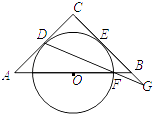 14. 将△ABC绕点B逆时针旋转到△A′BC′,使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为 cm2 .
14. 将△ABC绕点B逆时针旋转到△A′BC′,使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为 cm2 .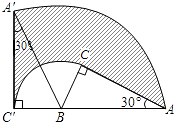 15. 矩形纸片ABCD中,AB=5,AC=3,将纸片折叠,使点B落在边CD上的B′处,折痕为AE.在折痕AE上存在一点P到边CD的距离与到点B的距离相等,则此相等距离为 .
15. 矩形纸片ABCD中,AB=5,AC=3,将纸片折叠,使点B落在边CD上的B′处,折痕为AE.在折痕AE上存在一点P到边CD的距离与到点B的距离相等,则此相等距离为 .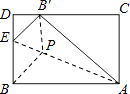
三、解答题
-
16. 先化简( ﹣ )÷ ,然后从不等式组 的解集中选取一个你喜欢的x的值代入求值.17. 如图,点A、F、C、D在同一直线上,AB∥DE,AC=DF,AB=DE.
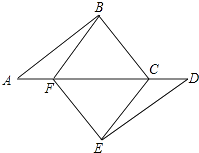 (1)、求证:四边形BCEF是平行四边形;(2)、若∠ABC=90°,AB=8,BC=6,当AF为何值时,四边形BCEF是菱形.18. 2017年8月1日是中国人民解放军成立90周年纪念日,某学校团委为此准备举行“学唱红歌”歌咏比赛,要确定一首喜欢人数最多的歌曲为每班必唱曲目,为此提供代号为A,B,C,D四首备选曲目让学生选择,经过抽样调查,并将采集的数据绘制如下两幅不完整的统计图.请根据图①、图②所提供的信息,解答下列问题:
(1)、求证:四边形BCEF是平行四边形;(2)、若∠ABC=90°,AB=8,BC=6,当AF为何值时,四边形BCEF是菱形.18. 2017年8月1日是中国人民解放军成立90周年纪念日,某学校团委为此准备举行“学唱红歌”歌咏比赛,要确定一首喜欢人数最多的歌曲为每班必唱曲目,为此提供代号为A,B,C,D四首备选曲目让学生选择,经过抽样调查,并将采集的数据绘制如下两幅不完整的统计图.请根据图①、图②所提供的信息,解答下列问题: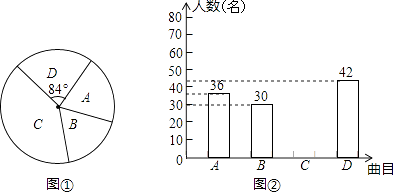 (1)、本次抽样调查的学生有名,其中选择曲目代号为A的学生所对应圆心角的度数为;(2)、请将图②补充完整;(3)、若该校共有1800名学生,根据抽样调查的结果估计全校共有多少名学生选择代号为C的曲目为必唱歌曲?19. 关于x的一元二次方程x2﹣3x﹣k=0有两个不相等的实数根.(1)、求k的取值范围;(2)、若这个方程有一个根为﹣2,求k的值和方程的另一个根.20. 我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)
(1)、本次抽样调查的学生有名,其中选择曲目代号为A的学生所对应圆心角的度数为;(2)、请将图②补充完整;(3)、若该校共有1800名学生,根据抽样调查的结果估计全校共有多少名学生选择代号为C的曲目为必唱歌曲?19. 关于x的一元二次方程x2﹣3x﹣k=0有两个不相等的实数根.(1)、求k的取值范围;(2)、若这个方程有一个根为﹣2,求k的值和方程的另一个根.20. 我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)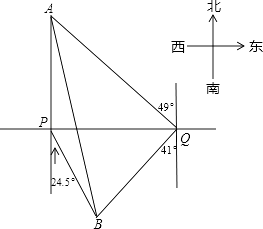 21. 顺丰快递公司派甲、乙两车从A地将一批物品匀速运往B地,甲出发0.5h后乙开始出发,结果比甲早1(h)到达B地,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,a表示A、B两地之间的距离.请结合图中的信息解决如下问题:
21. 顺丰快递公司派甲、乙两车从A地将一批物品匀速运往B地,甲出发0.5h后乙开始出发,结果比甲早1(h)到达B地,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,a表示A、B两地之间的距离.请结合图中的信息解决如下问题: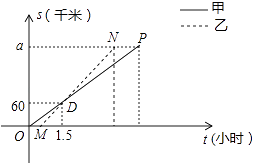 (1)、分别计算甲、乙两车的速度及a的值;(2)、乙车到达B地后以原速立即返回,请问甲车到达B地后以多大的速度立即匀速返回,才能与乙车同时回到A地?并在图中画出甲、乙两车在返回过程中离A地的距离S(km)与时间t(h)的函数图象.22. 如图1,直角∠EPF的顶点和正方形ABCD的顶点C重合,两直角边PE,PF分别和AB,AD所在的直线交于点E和F.易得△PBE≌△PDF,故结论“PE=PF”成立;
(1)、分别计算甲、乙两车的速度及a的值;(2)、乙车到达B地后以原速立即返回,请问甲车到达B地后以多大的速度立即匀速返回,才能与乙车同时回到A地?并在图中画出甲、乙两车在返回过程中离A地的距离S(km)与时间t(h)的函数图象.22. 如图1,直角∠EPF的顶点和正方形ABCD的顶点C重合,两直角边PE,PF分别和AB,AD所在的直线交于点E和F.易得△PBE≌△PDF,故结论“PE=PF”成立;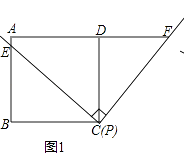 (1)、如图2,若点P在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?说明理由;
(1)、如图2,若点P在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?说明理由;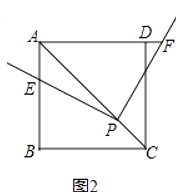 (2)、如图(3)将(2)中正方形ABCD改为矩形ABCD其他条件不变,若AB=m,BC=n,直接写出 的值.
(2)、如图(3)将(2)中正方形ABCD改为矩形ABCD其他条件不变,若AB=m,BC=n,直接写出 的值.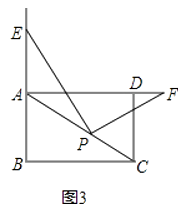 23. 如图,在平面直角坐标系中,已知矩形OABC的三个顶点A(0,10),B(8,10),C(8,0),过O、C两点的抛物线y=ax2+bx+c与线段AB交于点D,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.
23. 如图,在平面直角坐标系中,已知矩形OABC的三个顶点A(0,10),B(8,10),C(8,0),过O、C两点的抛物线y=ax2+bx+c与线段AB交于点D,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.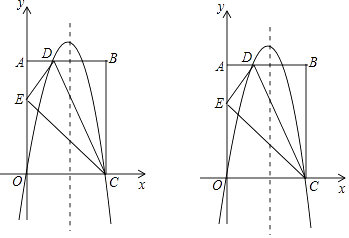 (1)、求AD的长及抛物线的解析式;(2)、一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒.请问当t为何值时,以P、Q、C为顶点的三角形是等腰三角形?(3)、若点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M、N、C、E为顶点四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
(1)、求AD的长及抛物线的解析式;(2)、一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒.请问当t为何值时,以P、Q、C为顶点的三角形是等腰三角形?(3)、若点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M、N、C、E为顶点四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.