河南省商丘市柘城县2016-2017学年中考五模数学考试试卷

试卷更新日期：2017-08-22 类型：中考模拟

进入出卷网下载

一、选择题

1. $- \frac{1}{2}$ 的倒数的绝对值是（）

A、1 B、﹣2 C、±2 D、2

查看试题解析
2. 自成都地铁4号线开通以来，成都地铁1、2、4号线线网客流增加明显，再遇到春季糖酒会、桃花节、通勤客流等三股主要客流汇集，2016年3月25日，成都地铁再创单日线网客流历史新高，达到1738200乘次，用科学记数法表示1738200为（保留三个有效数字）（　　）

A、1.74×10⁶ B、1.73×10⁶ C、17.4×10⁵ D、17.3×10⁵

查看试题解析
3. 已知x²﹣3x﹣4=0，则代数式 $\frac{x}{x^{2} - x - 4}$ 的值是（）

A、3 B、2 C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
4. 小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（）

A、①，② B、①，④ C、③，④ D、②，③

查看试题解析
5. 一只蚂蚁在如图所示的树枝上寻觅食物，假定蚂蚁在每个岔路口都会随即地选择一条路径，则它获得食物的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
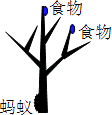6. 如图，点A（2，t）在第一象限，OA与x轴所夹锐角为α，tanα=2，则t值为（）

A、4 B、3 C、2 D、1

查看试题解析
7. 如图，有16个格点，每个格点小正方形的面积为1，给图中间的小正方形内任意投点P，则点P落在图中阴影部分的概率为（）

A、 $\frac{5}{6}$ B、 $\frac{7}{8}$ C、 $\frac{9}{10}$ D、 $\frac{11}{12}$

查看试题解析
8. 如图，AB是圆O的直径，DB，DC分别切圆O于点B，C，若∠ACE=25°，则∠D的度数是（）

A、50° B、55° C、60° D、65°

查看试题解析
9. 三角板ABC中，∠ACB=90°，∠B=30°，AC=2 $\sqrt{3}$ ，三角板绕直角顶点C逆时针旋转，当点A的对应点A′落在AB边的起始位置上时即停止转动，则B点转过的路径长为（）

A、 $\frac{3}{2}$ π B、 $\frac{4}{3} \sqrt{3}$ π C、2π D、3π

查看试题解析
10.
如图，正方形ABCD中，以AD为底边作等腰△ADE，将△ADE沿DE折叠，点A落到点F处，连接EF刚好经过点C，再连接AF，分别交DE于G，交CD于H．在下列结论中：
①△ABM≌△DCN；②∠DAF=30°；③△AEF是等腰直角三角形；④EC=CF；⑤S_△HCF=S_△ADH ，
其中正确的结论有（）

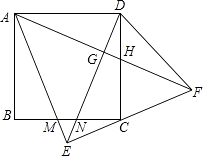A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 计算： $\frac{\sqrt{3}}{2}$ ﹣ $\sqrt{\frac{1}{3}}$ = ．

查看试题解析
12. 如图，在△ABC中，AB=AC=10，点D是边BC上一动点（不与B、C重合），∠ADE=∠B=α，DE交AC于点E，且cosα= $\frac{4}{5}$ ，则线段CE的最大值为．

查看试题解析
13.
如图，点A的坐标为（﹣4，0），直线y= $\sqrt{3}$ x+n与坐标轴交于点B、C，连接AC，如果∠ACD=90°，则n的值为．

查看试题解析
14. 如图，在平面直角坐标系中，A、B两点分别在x轴、y轴上，OA=3，OB=4，连接AB．点P在平面内，若以点P、A、B为顶点的三角形与△AOB全等（点P与点O不重合），则点P的坐标为．

查看试题解析

三、解答题

15. 先化简，再求值： $(\frac{x^{2} + 4}{x} + 4) \div \frac{x^{2} - 4}{x^{2} - 2 x}$ ﹣ $\frac{x - x^{2}}{x - 1}$ ，然后在0，1，2，3中选一个你认为合适的x值，代入求值．

查看试题解析
16. 如图，菱形ABCD的边长为2cm，∠DAB=60°．点P从A点出发，以 $\sqrt{3}$ cm/s的速度，沿AC向C作匀速运动；与此同时，点Q也从A点出发，以1cm/s的速度，沿射线AB作匀速运动．当P运动到C点时，P、Q都停止运动．设点P运动的时间为ts．

(1)、当P异于A、C时，请说明PQ∥BC；

(2)、以P为圆心、PQ长为半径作圆，请问：在整个运动过程中，t为怎样的值时，⊙P与边BC分别有1个公共点和2个公共点？

查看试题解析
17. 某中学开展菜市场菜价调查活动，以锻炼同学们的生活能力．调查一共连续7天，每天调查3次，第一次8：00由各班的A小组调查，第二次13：00由B小组调查，第三次17：00由C小组调查．调查完后分析当天的菜价波动情况，七天调查结束后整理数据，就得出了菜价最便宜的某一时段．下面是同学们的一些调查情况，请你帮忙分析数据：
第1天菜价调查情况（单位：元/千克）第2﹣5天平均菜价（单位：元/千克）

(1)、根据“第2﹣5天平均菜价”图来分析：哪种蔬果价格最便宜？

(2)、从第一天的调查情况来看，哪种蔬果的价格波动最小？请通过计算说明．

(3)、计算苹果、白菜、土豆在1﹣5天的平均菜价．

(4)、根据上面两个图来分析：在3﹣5天中的哪一天的哪一时段购买苹果最省钱？

查看试题解析
18.
如图所示，某工程队准备在山坡（山坡视为直线l）上修一条路，需要测量山坡的坡度，即tanα的值．测量员在山坡P处（不计此人身高）观察对面山顶上的一座铁塔，测得塔尖C的仰角为37°，塔底B的仰角为26.6°．已知塔高BC=80米，塔所在的山高OB=220米，OA=200米，图中的点O、B、C、A、P在同一平面内，求山坡的坡度．（参考数据sin26.6°≈0.45，tan26.6°≈0.50；sin37°≈0.60，tan37°≈0.75）

查看试题解析
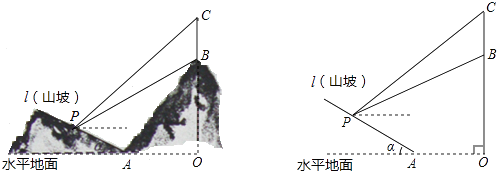19.
已知，直线l₁：y=﹣x+n过点A（﹣1，3），双曲线C：y= $\frac{m}{x}$ （x＞0），过点B（1，2），动直线l₂：y=kx﹣2k+2（常数k＜0）恒过定点F．

(1)、求直线l₁ ，双曲线C的解析式，定点F的坐标；

(2)、在双曲线C上取一点P（x，y），过P作x轴的平行线交直线l₁于M，连接PF．求证：PF=PM．

(3)、若动直线l₂与双曲线C交于P₁ ， P₂两点，连接OF交直线l₁于点E，连接P₁E，P₂E，求证：EF平分∠P₁EP₂ ．

查看试题解析
20. 甲乙两件服装的进价共500元，商场决定将甲服装按30%的利润定价，乙服装按20%的利润定价，实际出售时，两件服装均按9折出售，商场卖出这两件服装共获利67元．

(1)、求甲乙两件服装的进价各是多少元；

(2)、由于乙服装畅销，制衣厂经过两次上调价格后，使乙服装每件的进价达到242元，求每件乙服装进价的平均增长率；

(3)、若每件乙服装进价按平均增长率再次上调，商场仍按9折出售，定价至少为多少元时，乙服装才可获得利润（定价取整数）．

查看试题解析
21. △ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．

(1)、
观察猜想
如图1，当点D在线段BC上时，
①BC与CF的位置关系为：．
②BC，CD，CF之间的数量关系为：；（将结论直接写在横线上）

(2)、
数学思考
如图2，当点D在线段CB的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．

(3)、
拓展延伸
如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若已知AB=2 $\sqrt{2}$ ，CD= $\frac{1}{4}$ BC，请求出GE的长．

查看试题解析
22.
如图，抛物线y=ax²+bx+c（a、b、c为常数，a≠0）经过点A（﹣1，0），B（5，﹣5），C（6，0）

(1)、求抛物线的解析式；

(2)、如图，在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大？若存在，请求出点P的坐标；若不存在，请说明理由．

(3)、若点Q为抛物线的对称轴上的一个动点，试指出使△QAB为等腰三角形的点Q一共有几个？并请你求出其中一个点Q的坐标．

查看试题解析