河南省商丘市柘城县2016-2017学年中考模拟数学考试试卷
试卷更新日期:2017-08-22 类型:中考模拟
一、选择题
-
1. (﹣2)×3的结果是( )A、﹣5 B、1 C、﹣6 D、62. 据报道,某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水300 000吨.将300 000用科学记数法表示应为( )A、0.3×106 B、3×105 C、3×106 D、30×1043. 某几何体的三视图如图,则该几何体是( )
 A、三棱柱 B、长方体 C、圆柱 D、圆锥4. 不等式组 的解集是( )A、 <x≤2 B、﹣ <x<2 C、﹣ <x≤2 D、﹣ ≤x≤25. 正方形的对称轴的条数为( )A、1 B、2 C、3 D、46. 在半径为2的圆中,弦AB的长为2,则 的长等于( )A、 B、 C、 D、7. 已知某校女子田径队23人年龄的平均数和中位数都是13岁,但是后来发现其中一位同学的年龄登记错误,将14岁写成15岁,经重新计算后,正确的平均数为a岁,中位数为b岁,则下列结论中正确的是( )A、a<13,b=13 B、a<13,b<13 C、a>13,b<13 D、a>13,b=138. 如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )
A、三棱柱 B、长方体 C、圆柱 D、圆锥4. 不等式组 的解集是( )A、 <x≤2 B、﹣ <x<2 C、﹣ <x≤2 D、﹣ ≤x≤25. 正方形的对称轴的条数为( )A、1 B、2 C、3 D、46. 在半径为2的圆中,弦AB的长为2,则 的长等于( )A、 B、 C、 D、7. 已知某校女子田径队23人年龄的平均数和中位数都是13岁,但是后来发现其中一位同学的年龄登记错误,将14岁写成15岁,经重新计算后,正确的平均数为a岁,中位数为b岁,则下列结论中正确的是( )A、a<13,b=13 B、a<13,b<13 C、a>13,b<13 D、a>13,b=138. 如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )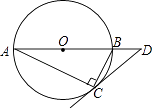 A、25° B、40° C、50° D、65°9. 某小区为了排污,需铺设一段全长为720米的排污管道,为减少施工对居民生活的影响,须缩短施工时间,实际施工时每天的工作效率比原计划提高20%,结果提前2天完成任务.设原计划每天铺设x米,下面所列方程正确的是( )A、 ﹣ =2 B、 ﹣ =2 C、 ﹣ =2 D、 =10. 如图,边长为1的正方形ABCD中,点E在CB的延长线上,连接ED交AB于点F,AF=x(0.2≤x≤0.8),EC=y.则在下面函数图象中,大致能反映y与x之间函数关系的是( )
A、25° B、40° C、50° D、65°9. 某小区为了排污,需铺设一段全长为720米的排污管道,为减少施工对居民生活的影响,须缩短施工时间,实际施工时每天的工作效率比原计划提高20%,结果提前2天完成任务.设原计划每天铺设x米,下面所列方程正确的是( )A、 ﹣ =2 B、 ﹣ =2 C、 ﹣ =2 D、 =10. 如图,边长为1的正方形ABCD中,点E在CB的延长线上,连接ED交AB于点F,AF=x(0.2≤x≤0.8),EC=y.则在下面函数图象中,大致能反映y与x之间函数关系的是( ) A、
A、 B、
B、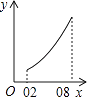 C、
C、 D、
D、
二、填空题
-
11. 分解因式:2a2﹣4a+2= .12. 在四个完全相同的小球上分别写上1,2,3,4四个数字,然后装入一个不透明的口袋内搅匀,从口袋内取出一个球记下数字后作为点P的横坐标x,放回袋中搅匀,然后再从袋中取出一个球记下数字后作为点P的纵坐标y,则点P(x,y)落在直线y=﹣x+5上的概率是 .13. 一元二次方程(a+1)x2﹣ax+a2﹣1=0的一个根为0,则a= .14. 如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为O.以点C为圆心,BC为半径作弧AB,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是 .
 15. 如图,已知矩形ABCD,把矩形沿直线AC折叠,点B落在点E处,连接DE、BE,若△ABE是等边三角形,则 = .
15. 如图,已知矩形ABCD,把矩形沿直线AC折叠,点B落在点E处,连接DE、BE,若△ABE是等边三角形,则 = .
三、解答题
-
16. 计算:(π﹣1)0+|2﹣ |﹣( )﹣1+ .17. 如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点.点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.
 (1)、求证:四边形AMDN是平行四边形;(2)、填空:①当AM的值为时,四边形AMDN是矩形;
(1)、求证:四边形AMDN是平行四边形;(2)、填空:①当AM的值为时,四边形AMDN是矩形;②当AM的值为时,四边形AMDN是菱形.
18. 在读书月活动中,学校准备购买一批课外读物,为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
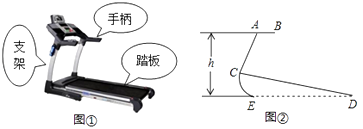
(1)、本次调查中,一共调查了多少名同学;(2)、条形统计图中,m,n的值;(3)、扇形统计图中,求出艺术类读物所在扇形的圆心角的度数;(4)、学校计划购买课外读物6000册,请根据样本数据,估计学校应购买其他类读物多少册?19. 图①、②分别是某种型号跑步机的实物图与示意图,已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到0.1m).(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)
 20. 如图,一次函数y=kx+b与反比例函数 的图象交于A(m,6),B(3,n)两点.
20. 如图,一次函数y=kx+b与反比例函数 的图象交于A(m,6),B(3,n)两点. (1)、求一次函数的解析式;(2)、根据图象直接写出 的x的取值范围;(3)、求△AOB的面积.21. 网络购物越来越方便快捷,远方的朋友通过网购就可以迅速品尝到茂名的新鲜荔枝,同时也增加了种植户的收入,种植户老张去年将全部荔枝按批发价卖给水果商,收入6万元,今年的荔枝产量比去年增加2000千克,计划全部采用互联网销售,网上销售比去年的批发价高50%,若按此价格售完,今年的收入将达到10.8万元.(1)、去年的批发价和今年网上售价分别是多少?(2)、若今年老张按(1)中的网上售价销售,则每天的销量相同,20天恰好可将荔枝售完,经调查发现,当网上售价每上升0.1元/千克,每日销量将减少5千克,将网上售价定为多少,才能使日销量收入最大?22. 数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)、求一次函数的解析式;(2)、根据图象直接写出 的x的取值范围;(3)、求△AOB的面积.21. 网络购物越来越方便快捷,远方的朋友通过网购就可以迅速品尝到茂名的新鲜荔枝,同时也增加了种植户的收入,种植户老张去年将全部荔枝按批发价卖给水果商,收入6万元,今年的荔枝产量比去年增加2000千克,计划全部采用互联网销售,网上销售比去年的批发价高50%,若按此价格售完,今年的收入将达到10.8万元.(1)、去年的批发价和今年网上售价分别是多少?(2)、若今年老张按(1)中的网上售价销售,则每天的销量相同,20天恰好可将荔枝售完,经调查发现,当网上售价每上升0.1元/千克,每日销量将减少5千克,将网上售价定为多少,才能使日销量收入最大?22. 数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).


(1)、初步尝试如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)、类比发现如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)、深入探究如图3,若AD=3AB,探究得: 的值为常数t,则t=
23. 如图所示,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根. (1)、求直线AB和OB的解析式.(2)、求抛物线的解析式.(3)、若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.问△BOD的面积是否存在最大值?若存在,求出这个最大值并写出此时点D的坐标;若不存在说明理由.
(1)、求直线AB和OB的解析式.(2)、求抛物线的解析式.(3)、若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.问△BOD的面积是否存在最大值?若存在,求出这个最大值并写出此时点D的坐标;若不存在说明理由.