河南省普通高中2016-2017学年中考模拟数学考试试卷（预测二）

试卷更新日期：2017-08-22 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣ $\sqrt{2}$ 的倒数是（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\sqrt{2}$ C、﹣ $\sqrt{2}$ D、﹣ $\frac{\sqrt{2}}{2}$

查看试题解析
2. 用一根6米长的绳子围成一个平行四边形，其中一边长1.6米，则其邻边长为（）

A、1.2米 B、1.4米 C、1.6米 D、1.8米

查看试题解析
3. 在函数y= $\frac{2}{\sqrt{x - 2}}$ 中，自变量x的取值范围是（）

A、x＞2 B、x≥2 C、x＜2 D、x≤2

查看试题解析
4. 在△ABC中，若∠A的补角是85°，∠B的余角是65°，则∠C的度数为（）

A、60° B、65° C、80° D、85°

查看试题解析
5. 估计2 $\sqrt{13}$ ﹣1的值介于（）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看试题解析
6. 计算：（2x²）³﹣6x³（x³+2x²+x）=（）

A、﹣12x⁵﹣6x⁴ B、2x⁶+12x⁵+6x⁴ C、x²﹣6x﹣3 D、2x⁶﹣12x⁵﹣6x⁴

查看试题解析
7. 在平面直角坐标系中，点A的坐标是（﹣1，0），点B的坐标是（3，0），在y轴的正半轴上取一点C，使A、B、C三点确定一个圆，且使AB为圆的直径，则点C的坐标是（）

A、（0， $\sqrt{3}$ ） B、（ $\sqrt{3}$ ，0） C、（0，2） D、（2，0）

查看试题解析
8. 如图，转盘被划分成4个相同的小扇形，并分别标上数字1，2，3，4，分别转动两次转盘，转盘停止后，指针所指向的数字作为直角坐标系中M点的坐标（第一次作横坐标，第二次作纵坐标），指针如果指向分界线上，认为指向左侧扇形的数字，则点M落在直线y=x的下方的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{3}{8}$ C、 $\frac{1}{2}$ D、 $\frac{5}{8}$

查看试题解析
9. 如图，点A、B的坐标分别为（2，0）、（0，2），分别以A、B为圆心，大于 $\frac{1}{2}$ AB的长为半径画弧，两弧相交于点M，N，作直线MN，交函数y= $\frac{k}{x}$ （k＞4）的图象于点C，则△ABC的面积为（）

A、k B、 $\sqrt{k}$ C、k﹣2 D、2 $\sqrt{k}$ ﹣2

查看试题解析
10. 在下列命题中：①平行四边形的一组对边相等；②线段垂直平分线上的点到这条线段两个端点的距离相等；③矩形的两条对角线相等；④四边形相等的四边形是菱形；⑤在直角三角形中，斜边上的中线等于斜边的一半；其逆命题是真命题的是（）

A、①②④ B、②③④ C、②④⑤ D、①③⑤

查看试题解析

二、填空题

11. 计算：（ $\frac{3}{8}$ ﹣ $\frac{5}{6}$ ）×（﹣24）= ．

查看试题解析
12. 不等式组 ${\begin{matrix} - 2 x - 1 \leq 7 \\ - \frac{1}{2} x > 1 \end{matrix}$ 的最大整数解为．

查看试题解析
13. 抛物线L：y=﹣ $\frac{1}{2}$ （x+t）（x﹣t+4）与x轴只有一个交点，则抛物线L与x轴的交点坐标是．

查看试题解析
14. 如图，在△ABC中，∠ACB=90°，AC=2，∠B=30°，以AC为直径作圆交AB于点E，则图中阴影部分的面积为．

查看试题解析
15. 如图，四边形ABCD为正方形，边长为4，E为AD延长线上一点，DE=x（0＜x＜4），在AE上取一点M，连接CM，将△CME沿CM对折，若点E恰落在线段AB上的点F处，则AM= ．

查看试题解析

三、解答题

16. $\frac{x - 4}{x - 2}$ ÷（ $\frac{x + 2}{x^{2} - 2 x}$ ﹣ $\frac{x - 1}{x^{2} - 4 x + 4}$ ），其中x满足x²=2x﹣2017．

查看试题解析
17. 某校为了解全校2000名学生每周去图书馆时间的情况，随机调查了其中的100名学生，对这100名学生每周去图书馆的时间x（单位：小时）进行了统计．根据所得数据绘制了一幅不完整的统计图，并知道每周去图书馆的时间在6≤x＜8小时的学生人数占20%．根据以上信息及统计图解答下列问题：

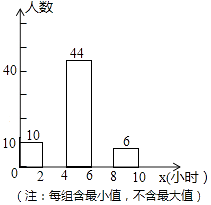(1)、本次调查属于调查，样本容量是；

(2)、请补全频数分布直方图中空缺的部分；

(3)、若从这100名学生中随机抽取1名学生，求抽取的这个学生每周去图书馆的时间恰好在8﹣10小时的概率；

(4)、估计全校学生每周去图书馆的时间不少于6小时的人数．

查看试题解析
18. 如图．AB是⊙O的直径，E为弦AP上一点，过点E作EC⊥AB于点C，延长CE至点F，连接FP，使∠FPE=∠FEP，CF交⊙O于点D．

(1)、证明：FP是⊙O的切线；

(2)、若四边形OBPD是菱形，证明：FD=ED．

查看试题解析
19. 如图，甲乙两人在游泳池A处发现游泳池中的P处有人求救，甲立即跳入池中去救人，速度为1米/秒，乙以3.5米/秒的速度沿游泳池边跑到距A不远处的B处，捡起一个游泳圈再跳入池中去救人，甲游了20秒到达P处，两秒后乙到达P处．若∠PAB与∠PBC互余，且cos∠PBC= $\frac{3}{5}$ ，求乙的游泳速度．

查看试题解析
20. 某厂生产一种工具，据市场调查，若按每个工具280元销售时，每月可销售300个，若销售单价每降低1元，每月可多售出2个，据统计，每个工具的固定成本Q（元）与月销售y（个）满足如下关系：
月销量y（个）
100
160
240
320
每个工具的固定成本Q（元）
96
60
40
30

(1)、写出月产销量y（个）与销售单价x（元）之间的函数关系式；

(2)、求每个玩具的固定成本Q（元）与月产销量y（个）之间的函数关系式；

(3)、若该厂这种玩具的月产销量不超过400个，则每个玩具的固定成本至少为多少元？销售单价最低为多少元？

查看试题解析
21. 如图，在平面直角坐标系中，矩形ABCD的顶点A、D在坐标轴上，其坐标分别为（2，0），（0，4），对角线AC⊥x轴．

(1)、求直线DC对应的函数解析式

(2)、若反比例函数y= $\frac{k}{x}$ （k＞0）的图象经过DC的中点M，请判断这个反比例函数的图象是否经过点B，并说明理由．

查看试题解析
22. 根据要求回答问题：

(1)、
发现
如图1，直线l₁∥l₂ ， l₁和l₂的距离为d，点P在l₁上，点Q在l₂上，连接PQ，填空：PQ长度的最小值为.

(2)、
应用
如图2，在四边形ABCD中，DC∥AB，AD⊥AB，DC=2，AD=4，AB=6，点M在线段AD上，AM=3MD，点N在直线BC上，连接MN，求MN长度的最小值

(3)、
拓展
如图3，在四边形ABCD中，DC∥AB，AD⊥AB，DC=2，AD=4，AB=6，点M在线段AD上任意一点，连接MC并延长到点E，使MC=CE，以MB和ME为边作平行四边形MBNE，请直接写出线段MN长度的最小值

查看试题解析
23.
如图，抛物线y=x²+bx+c与x轴交于点A，B，与y轴交于点C，其中点A在y轴的左侧，点C在x轴的下方，且OA=OC=5．

(1)、求抛物线对应的函数解析式；

(2)、点P为抛物线对称轴上的一动点，当PB+PC的值最小时，求点P的坐标；

(3)、在（2）条件下，点E为抛物线的对称轴上的动点，点F为抛物线上的动点，以点P、E、F为顶点作四边形PEFM，当四边形PEFM为正方形时，请直接写出坐标为整数的点M的坐标．

查看试题解析

月销量y（个）	100	160	240	320
每个工具的固定成本Q（元）	96	60	40	30