河北省保定市高阳县2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-03-13 类型：期中考试

进入出卷网下载

一、单选题

1. 要使二次根式 $\sqrt{2 x + 3}$ 有意义，字母x的取值必须满足（）

A、x≥0 B、 $x \geq \frac{3}{2}$ C、 $x \geq - \frac{2}{3}$ D、 $x \geq - \frac{3}{2}$

查看试题解析
2. 下列运算错误的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{2} \cdot \sqrt{3} = \sqrt{6}$ C、 $\sqrt{6} \div \sqrt{2} = \sqrt{3}$ D、 ${(- \sqrt{2})}^{2} = 2$

查看试题解析
3. 下列各点在函数y=1-2x的图象上的是（）

A、 $(0, 2)$ B、 $(1, 0)$ C、 $(1, - 1)$ D、 $(2, - 1)$

查看试题解析
4. 下列四组线段中，可以构成直角三角形的是（　　）

A、4，5，6 B、1.5，2，2.5 C、2，3，4 D、1， $\sqrt{2}$ ， 3

查看试题解析
5. 下列各式属于最简二次根式的有（）

A、 $\sqrt{8}$ B、 $\sqrt{x^{2} + 1}$ C、 $\sqrt{y^{3}}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
6. 如图，下列哪组条件不能判定四边形ABCD是平行四边形（）

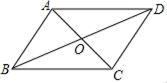A、AB∥CD ， AB＝CD B、AB∥CD ， AD∥BC C、OA＝OC ， OB＝OD D、AB∥CD ， AD＝BC

查看试题解析
7. 点P（3，－1）、Q（－3，－1）、R（ $\frac{5}{2}$ ，0）、S（ $\frac{1}{2}$ ，4）中，在函数y＝－2x＋5的图象上的点有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，在▱ABCD中，已知AD=5cm，AB=3cm，AE平分∠BAD交BC边于点E，则EC等于（）

A、1cm B、2cm C、3cm D、4cm

查看试题解析
9. 如图，平行四边形ABCD的周长为24cm ， AC与BD相交于点O ， OE⊥AC交AD于E ，则△DCE的周长为（）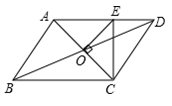

A、4cm B、16cm C、12cm D、24cm

查看试题解析
10. 如图，OP=1，过点P作PP₁⊥OP且PP₁=1，得OP₁= $\sqrt{2}$ ；再过点P₁作P₁P₂⊥OP₁且P₁P₂=1，得OP₂= $\sqrt{3}$ ；又过点P₂作P₂P₃⊥OP₂且P₂P₃=1，得OP₃=2……依此法继续作下去，得OP₂₀₁₇=（）

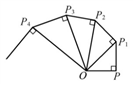A、 $\sqrt{2015}$ B、 $\sqrt{2016}$ C、 $\sqrt{2017}$ D、 $\sqrt{2018}$

查看试题解析
11.
如图，长为8cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3cm至D点，则橡皮筋被拉长了（　　）

A、2cm B、3cm C、4cm D、5cm

查看试题解析
12. 如图所示，在数轴上点A所表示的数为 $a$ ，则 $a$ 的值为（）

A、 $- \sqrt{5}$ B、 $1 - \sqrt{5}$ C、 $- 1 - \sqrt{5}$ D、 $- 1 + \sqrt{5}$

查看试题解析
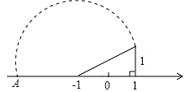13. 星期天晚饭后，小红从家里出去散步，如图描述了她散步过程中离家的距离s（米）与散步所用时间t（分）之间的关系．依据图象，下面描述符合小红散步情景的是（）．

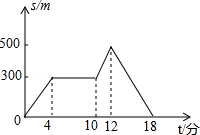A、从家出发，到了一个公共阅报栏，看了一会儿报，就回家了 B、从家出发，到了一个公共阅报栏，看了一会儿报后，继续向前走了一段，然后回家了 C、从家出发，一直散步（没有停留），然后回家了 D、从家出发，散了一会儿步，就找同学去了，18min后才开始返回

查看试题解析
14. 计算( $\sqrt{10}$ +3)²⁰¹⁰( $\sqrt{10}$ -3)²⁰⁰⁹的结果是（）

A、 $\sqrt{10}$ -3 B、3 C、-3 D、 $\sqrt{10}$ +3

查看试题解析
15. 如图，D是△ABC内一点，BD⊥CD，AD＝6，BD＝4，CD＝3，E，F，G，H，分别是AB，AC，CD，BD的中点，则四边形EFGH的周长是（）

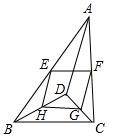A、7 B、9 C、10 D、11

查看试题解析
16. 如图，在4×4方格中作以AB为一边的Rt△ABC，要求点C也在格点上，这样的Rt△ABC能作出（）

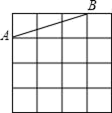A、2个 B、3个 C、4个 D、6个

查看试题解析
17. 如图所示，实数a、b在数轴上的位置化简 $\sqrt{a^{2}} - \sqrt{b^{2}} + \sqrt{{(a - b)}^{2}}$ 的结果是（）

A、﹣2a B、﹣2b C、0 D、2a﹣2b

查看试题解析

二、填空题

18. 计算 $\sqrt{40}$ ÷ $\sqrt{5}$ 的结果是．

查看试题解析
19. “平行四边形两组对边分别相等”的逆命题是，它是（填“真命题”或“假命题”）．

查看试题解析
20.
如图，将两条宽度都为3的纸条重叠在一起，使∠ABC=60°，则四边形ABCD的面积为．

查看试题解析

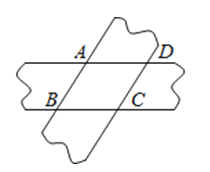
三、解答题

21.

(1)、 $\sqrt{24}$ （- $\sqrt{\frac{2}{3}}$ +3 $\sqrt{\frac{5}{6}}$ + $\sqrt{5}$ ）

(2)、（4+ $\sqrt{5}$ ）（4- $\sqrt{5}$ ）-（2 $\sqrt{2}$ - $\sqrt{3}$ ）²

查看试题解析
22. 画出函数y＝2x－1的图象．

(1)、列表：

x

…

－1

0

1

…

y

…

…

(2)、描点并连线；

(3)、判断点A(－3，－5)，B(2，－3)，C(3，5)是否在函数y＝2x－1的图象上？

(4)、若点P(m，9)在函数y＝2x－1的图象上，求出m的值．

查看试题解析
23. 如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD，等边△ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．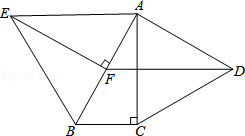

(1)、试说明AC=EF；

(2)、求证：四边形ADFE是平行四边形．

查看试题解析
24. 如图，正方形ABCD的边长为2 $\sqrt{2}$ ，对角线AC、BD相交于点O，E是OC的中点，连接BE，过点A作AM⊥BE于点M，交BD于点F．

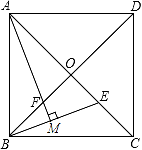(1)、求证：AF=BE；

(2)、求点E到BC边的距离．

查看试题解析
25. 观察下列等式：
① $\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ；

② $\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；

③ $\frac{1}{\sqrt{4} + \sqrt{3}} = \frac{\sqrt{4} - \sqrt{3}}{(\sqrt{4} + \sqrt{3}) (\sqrt{4} - \sqrt{3})} = \sqrt{4} - \sqrt{3}$ ；……

回答下列问题：

(1)、利用你观察到的规律，化简： $\frac{1}{\sqrt{23} + \sqrt{22}}$

(2)、计算： $\frac{1}{1 + \sqrt{2}}$ + $\frac{1}{\sqrt{2} + \sqrt{3}}$ + $\frac{1}{\sqrt{3} + \sqrt{4}}$ +……+ $\frac{1}{\sqrt{99} + \sqrt{100}}$

查看试题解析
26. 问题背景：
在△ABC中，AB、BC、AC三边的长分别为 $\sqrt{5}$ 、 $\sqrt{10}$ 、 $\sqrt{13}$ ，求这个三角形的面积．

小辉同学在解答这道题时．先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处）．如图①所示．这样不需求△ABC的高．而借用网格就能计算出它的面积．

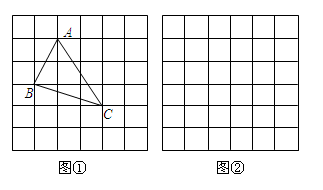(1)、请你将△ABC的面积直接填写在横线上；
思维拓展：

(2)、我们把上述求△ABC面积的方法叫做构图法．若△ABC三边的长分别为 $\sqrt{2}$ ， $\sqrt{13}$ ， $\sqrt{17}$ ，请利用图②的正方形网格（每个小正方形的边长为1）画出相应的△ABC ．并求出它的面积
探索创新：

(3)、若△ABC三边的长分别为 $\sqrt{5}$ a、2 $\sqrt{2}$ a、 $\sqrt{17}$ a（a＞0），请利用图（2）的正方形网格（每个小正方形的边长为a）画出相应的△ABC ．并求出它的面积．

(4)、若△ABC三边的长分别为 $\sqrt{m^{2} + 16 n^{2}}$ 、 $\sqrt{9 m^{2} + 4 n^{2}}$ ，2 $\sqrt{m^{2} + n^{2}}$ （m＞0，n＞0，且m≠n），试运用构图法求出这个三角形的面积．

查看试题解析

x	…	－1	0	1	…
y	…				…