河南省南阳市邓州市2016-2017学年中考一模数学考试试卷
试卷更新日期:2017-08-22 类型:中考模拟
一、选择题
-
1. ﹣2的相反数是( )A、2 B、 C、﹣ D、﹣22.
中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,满载排水量为67500吨,将67500用科学记数法表示为( )
 A、6.75×104吨 B、67.5×103吨 C、0.675×103吨 D、6.75×10﹣4吨3. 如图是两个相同的正方体和一个圆锥形组成的立体图形,其主视图是( )
A、6.75×104吨 B、67.5×103吨 C、0.675×103吨 D、6.75×10﹣4吨3. 如图是两个相同的正方体和一个圆锥形组成的立体图形,其主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 为了了解某班学生每天使用零花钱的情况,班主任随机调查了15名同学,调查的结果如下表:
4. 为了了解某班学生每天使用零花钱的情况,班主任随机调查了15名同学,调查的结果如下表:人数
1
3
5
4
2
每天零花钱(元)
0
1
3
4
5
对于表中数据,下列说法正确的是( )
A、中位数是3元 B、平均数是2.5元 C、方差是4 D、众数是5元5. 关于x的一元二次方程(m﹣2)2x2+(2m+1)x+1=0有两个不相等的实数根,则m的取值范围是( )A、m< B、m> 且m≠2 C、m≤ D、m≥ 且m≠26. 如图,一副分别含有30°和45°角的两个直角三角板,拼成如图所示,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( )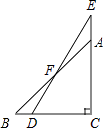 A、10° B、15° C、25° D、30°7. 不等式2x+3≥1的解集在数轴上表示为( )A、
A、10° B、15° C、25° D、30°7. 不等式2x+3≥1的解集在数轴上表示为( )A、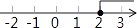 B、
B、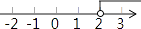 C、
C、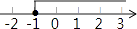 D、
D、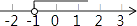 8. 下列运算正确的个数是( )
8. 下列运算正确的个数是( )①2a2﹣a2=a2;
② + =2 ;
③(π﹣3.14)0× =0;
④a2÷a× =a2;
⑤sin30°+cos60°= ;
⑥精确到万位6295382≈6.30×106 .
A、1 B、2 C、3 D、49. 如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2 ,则线段CE的长为( ) A、 B、8 C、2 D、910.
A、 B、8 C、2 D、910.如图,直角梯形AOCD的边OC在x轴上,O为坐标原点,CD垂直于x轴,D(5,4),AD=2.若动点E、F同时从点O出发,E点沿折线OA→AD→DC运动,到达C点时停止;F点沿OC运动,到达C点时停止,它们运动的速度都是每秒1个单位长度.设E运动x秒时,△EOF的面积为y(平方单位),则y关于x的函数图象大致为( )
 A、
A、 B、
B、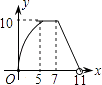 C、
C、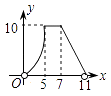 D、
D、
二、填空题
-
11. |﹣3|+(﹣1)2017= .12. 如图,将纸片ABCD沿PR翻折得到△PC′R,恰好C′P∥AB,C′R∥AD.若∠B=120°,∠D=50°,则∠C=度.
 13. 经过某十字路口的汽车,直行、向左转或向右转的可能性大小相同,则两辆汽车经过该十字路口都直行的概率为 .14. 双曲线y1、y2在第一象限的图象如图所示,y2= ,过y1上的任意一点A作x轴的平行线交y2于点B,交y轴于点C,如果S△AOB=4,那么y1的函数表达式是 .
13. 经过某十字路口的汽车,直行、向左转或向右转的可能性大小相同,则两辆汽车经过该十字路口都直行的概率为 .14. 双曲线y1、y2在第一象限的图象如图所示,y2= ,过y1上的任意一点A作x轴的平行线交y2于点B,交y轴于点C,如果S△AOB=4,那么y1的函数表达式是 . 15. 如图,矩形纸片ABCD中,AB=6,AD=10,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是 .
15. 如图,矩形纸片ABCD中,AB=6,AD=10,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是 .
三、解答题
-
16. 先化简,再求值:( ﹣ )÷ ,然后从﹣3≤x≤3的取值范围内选取一个合适的整数解作为x的值代入求值.17. 如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为 cm,AC=8cm,设运动时间为t秒.
 (1)、求证:NQ=MQ;(2)、填空:
(1)、求证:NQ=MQ;(2)、填空:①当t=时,四边形AMQN为菱形;
②当t=时,NQ与⊙O相切.
18. 为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:社团类别
人数
占总人数比例
球类
60
m
舞蹈
30
0.25
健美操
n
0.15
武术
12
0.1
 (1)、求样本容量及表格中m、n的值;(2)、请补全统计图;(3)、被调查的60个喜欢球类同学中有3人最喜欢足球,若该校有3000名学生,请估计该校最喜欢足球的人数.19.
(1)、求样本容量及表格中m、n的值;(2)、请补全统计图;(3)、被调查的60个喜欢球类同学中有3人最喜欢足球,若该校有3000名学生,请估计该校最喜欢足球的人数.19.如图,为了测量出楼房AC的高度,从距离楼底C处60 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1: 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°= ,cos = ,tan53°= , ≈1.732,结果精确到0.1米)
 20. 如图,一次函数y=kx+b与反比例函数y= (x>0)的图象交于A(m,6),B(n,3)两点.
20. 如图,一次函数y=kx+b与反比例函数y= (x>0)的图象交于A(m,6),B(n,3)两点. (1)、求一次函数的解析式;(2)、根据图象直接写出kx+6﹣ >0时,x的取值范围;(3)、若M是x轴上一点,S△MOB=S△AOB , 求点M的坐标.21. 某校为表彰在美术展览活动中获奖的同学,老师决定购买一些水笔和颜料盒作为奖品,请你根据图中所给的信息,解答下列问题;
(1)、求一次函数的解析式;(2)、根据图象直接写出kx+6﹣ >0时,x的取值范围;(3)、若M是x轴上一点,S△MOB=S△AOB , 求点M的坐标.21. 某校为表彰在美术展览活动中获奖的同学,老师决定购买一些水笔和颜料盒作为奖品,请你根据图中所给的信息,解答下列问题; (1)、求出每个颜料盒,每支水笔各多少元?(2)、若学校计划购买颜料盒和水笔共20个,所用费用不超过340元,则颜料盒至多购买多少个?(3)、恰逢商店举行优惠促销活动,具体办法如下:颜料盒按七折优惠,水笔10支以上超出部分按八折优惠,若学校决定购买同种数量的同一奖品,并且该奖品的数量超过10件,请你帮助分析,购买颜料盒合算还是购买水笔合算.22. 根据问题填空:(1)、
(1)、求出每个颜料盒,每支水笔各多少元?(2)、若学校计划购买颜料盒和水笔共20个,所用费用不超过340元,则颜料盒至多购买多少个?(3)、恰逢商店举行优惠促销活动,具体办法如下:颜料盒按七折优惠,水笔10支以上超出部分按八折优惠,若学校决定购买同种数量的同一奖品,并且该奖品的数量超过10件,请你帮助分析,购买颜料盒合算还是购买水笔合算.22. 根据问题填空:(1)、问题发现:
如图①,在等边三角形ABC中,点M为BC边上异于B、C的一点,以AM为边作等边三角形AMN,连接CN,NC与AB的位置关系为;
 (2)、
(2)、深入探究:
如图②,在等腰三角形ABC中,BA=BC,点M为BC边上异于B、C的一点,以AM为边作等腰三角形AMN,使∠ABC=∠AMN,AM=MN,连接CN,试探究∠ABC与∠ACN的数量关系,并说明理由;
 (3)、
(3)、拓展延伸:
如图③,在正方形ADBC中,AD=AC,点M为BC边上异于B、C的一点,以AM为边作正方形AMEF,点N为正方形AMEF的中点,连接CN,若BC=10,CN= ,试求EF的长.
 23.
23.如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4)与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
 (1)、求抛物线的解析式;(2)、若点F事直线BC上方的抛物线上的一个动点,是否存在点F,使四边形ABFC的面积为15?若存在,求出点F的坐标;若不存在,请说明理由;(3)、平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
(1)、求抛物线的解析式;(2)、若点F事直线BC上方的抛物线上的一个动点,是否存在点F,使四边形ABFC的面积为15?若存在,求出点F的坐标;若不存在,请说明理由;(3)、平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.