河北省2016-2017学年中考数学考试压轴试卷(一)
试卷更新日期:2017-08-22 类型:中考模拟
一、选择题
-
1. 如图,数轴上的A、B、C、D四点中,与数﹣ 表示的点最接近的是( )
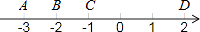 A、点A B、点B C、点C D、点D2. 下列运算正确的是( )A、a2⋅a3=a6 B、(a2)3=a6 C、(﹣ab2)6=a6b6 D、(a+b)2=a2+b23. 下列图形中,不是中心对称图形的是( )A、
A、点A B、点B C、点C D、点D2. 下列运算正确的是( )A、a2⋅a3=a6 B、(a2)3=a6 C、(﹣ab2)6=a6b6 D、(a+b)2=a2+b23. 下列图形中,不是中心对称图形的是( )A、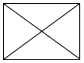 B、
B、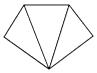 C、
C、 D、
D、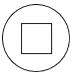 4. 的算术平方根是( )A、2 B、±2 C、 D、5. 要使分式有意义,则x的取值应满足( )A、x=﹣2 B、x≠2 C、x>﹣2 D、x≠﹣26. 在某校“我的中国梦”演讲比赛中,有9名学生参加比赛,他们决赛的最终成绩各不相同,其中的一名学生要想知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )A、众数 B、方差 C、平均数 D、中位数7. 将一张长与宽的比为2:1的长方形纸片按如图①、②所示的方式对折,然后沿图③中的虚线裁剪,得到图④,最后将图④的纸片再展开铺平,则所得到的图案是( )
4. 的算术平方根是( )A、2 B、±2 C、 D、5. 要使分式有意义,则x的取值应满足( )A、x=﹣2 B、x≠2 C、x>﹣2 D、x≠﹣26. 在某校“我的中国梦”演讲比赛中,有9名学生参加比赛,他们决赛的最终成绩各不相同,其中的一名学生要想知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )A、众数 B、方差 C、平均数 D、中位数7. 将一张长与宽的比为2:1的长方形纸片按如图①、②所示的方式对折,然后沿图③中的虚线裁剪,得到图④,最后将图④的纸片再展开铺平,则所得到的图案是( ) A、
A、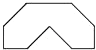 B、
B、 C、
C、 D、
D、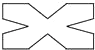 8. 如图几何体的俯视图是( )
8. 如图几何体的俯视图是( )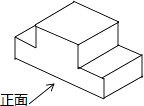 A、
A、 B、
B、 C、
C、 D、
D、 9. 下列等式从左到右的变形,属于因式分解的是( )A、a(x﹣y)=ax﹣ay B、x2+2x+1=x(x+2)+1 C、(x+1)(x+3)=x2+4x+3 D、x3﹣x=x(x+1)(x﹣1)10. △ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是( )A、3 B、6 C、9 D、1211. 解分式方程 + =3时,去分母后变形正确的是( )A、2+(x+2)=3(x﹣1) B、2﹣x+2=3(x﹣1) C、2﹣(x+2)=3 D、2﹣(x+2)=3(x﹣1)12. 将直角三角尺的直角顶点靠在直尺上,且斜边与这根直尺平行,那么,在形成的这个图中与∠α互余的角共有( )
9. 下列等式从左到右的变形,属于因式分解的是( )A、a(x﹣y)=ax﹣ay B、x2+2x+1=x(x+2)+1 C、(x+1)(x+3)=x2+4x+3 D、x3﹣x=x(x+1)(x﹣1)10. △ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是( )A、3 B、6 C、9 D、1211. 解分式方程 + =3时,去分母后变形正确的是( )A、2+(x+2)=3(x﹣1) B、2﹣x+2=3(x﹣1) C、2﹣(x+2)=3 D、2﹣(x+2)=3(x﹣1)12. 将直角三角尺的直角顶点靠在直尺上,且斜边与这根直尺平行,那么,在形成的这个图中与∠α互余的角共有( )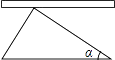 A、4个 B、3个 C、2个 D、1个13. 如图,点A是反比例函数y= (x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上.已知平行四边形ABCD的面积为6,则k的值为( )
A、4个 B、3个 C、2个 D、1个13. 如图,点A是反比例函数y= (x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上.已知平行四边形ABCD的面积为6,则k的值为( )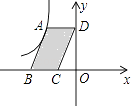 A、6 B、﹣6 C、3 D、﹣314. 如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论正确的是( )
A、6 B、﹣6 C、3 D、﹣314. 如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论正确的是( )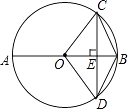 A、OE=BE B、 = C、△BOC是等边三角形 D、四边形ODBC是菱形15. 小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,求山高( )
A、OE=BE B、 = C、△BOC是等边三角形 D、四边形ODBC是菱形15. 小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,求山高( )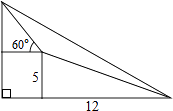 A、600﹣250 米 B、600 ﹣250米 C、350+350 米 D、500 米
A、600﹣250 米 B、600 ﹣250米 C、350+350 米 D、500 米二、填空题
-
16. 若|a|=20160 , 则a= .17. 如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为 .
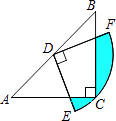 18.
18.在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动3个单位长度到达点A1 , 第二次将点A1向右移动6个单位长度到达点A2 , 第三次将点A2向左移动9个单位长度到达点A3 , 则A3表示的数是按照这种移动规律移动下去,第n次移动到点AN , 如果点AN与原点的距离不小于20,那么n的最小值是 .
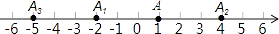
三、解答题
-
19. 计算:(﹣2015)0+|1﹣ |﹣2cos45°+ +(﹣ )﹣2 .20. 先化简,再求值: ,其中x= +1.21. 为了解今年初四学生的数学学习情况,某校在第一轮模拟测试后,对初四全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:
成绩
频数
频率
优秀
45
b
良好
a
0.3
合格
105
0.35
不合格
60
c
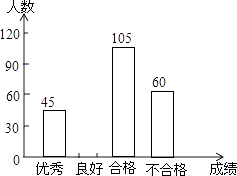 (1)、该校初四学生共有多少人?(2)、求表中a,b,c的值,并补全条形统计图.(3)、初四(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.22. 我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线y= 的一部分,请根据图中信息解答下列问题:
(1)、该校初四学生共有多少人?(2)、求表中a,b,c的值,并补全条形统计图.(3)、初四(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.22. 我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线y= 的一部分,请根据图中信息解答下列问题: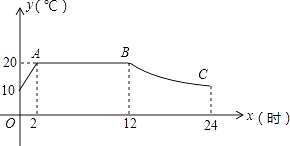 (1)、求k的值;(2)、恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?23. 已知一次函数y=﹣ x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
(1)、求k的值;(2)、恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?23. 已知一次函数y=﹣ x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.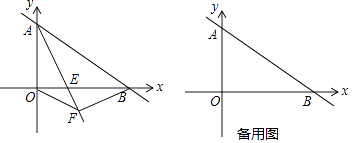 (1)、求点B的坐标;(2)、求直线AE的表达式;(3)、过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.24. 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5.OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)、求点B的坐标;(2)、求直线AE的表达式;(3)、过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.24. 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5.OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.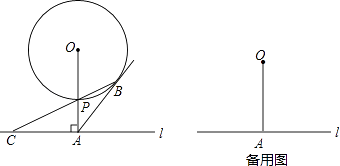 (1)、试判断线段AB与AC的数量关系,并说明理由;(2)、若PC=2 ,求⊙O的半径和线段PB的长;(3)、若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围.25. 抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)、试判断线段AB与AC的数量关系,并说明理由;(2)、若PC=2 ,求⊙O的半径和线段PB的长;(3)、若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围.25. 抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)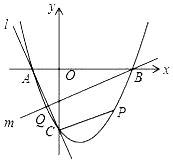 (1)、求抛物线的解析式;(2)、点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标(3)、直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标(3)、直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.