河北省唐山市玉田县2016-2017学年中考二模数学考试试卷
试卷更新日期:2017-08-22 类型:中考模拟
一、选择题
-
1. 9的绝对值是( )A、9 B、﹣9 C、 D、2.
如图是我国几家银行的标志,其中即是轴对称图形又是中心对称图形的有( )
 A、2个 B、3个 C、4个 D、5个3. 如图是一个水平放置的圆柱形物体,中间有一细棒,则此几何体的俯视图是( )
A、2个 B、3个 C、4个 D、5个3. 如图是一个水平放置的圆柱形物体,中间有一细棒,则此几何体的俯视图是( )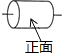 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、20170=0 B、 =±9 C、(x2)3=x5 D、3﹣1=5. 已知点P(a+1,2a﹣3)关于x轴的对称点在第一象限,则a的取值范围是( )A、a<﹣1 B、﹣1<a< C、﹣ <a<1 D、a>6. 小明在某商店购买商品A、B共两次,这两次购买商品A、B的数量和费用如表:
4. 下列计算正确的是( )A、20170=0 B、 =±9 C、(x2)3=x5 D、3﹣1=5. 已知点P(a+1,2a﹣3)关于x轴的对称点在第一象限,则a的取值范围是( )A、a<﹣1 B、﹣1<a< C、﹣ <a<1 D、a>6. 小明在某商店购买商品A、B共两次,这两次购买商品A、B的数量和费用如表:购买商品A的数量(个)
购买商品B的数量(个)
购买总费用(元)
第一次购物
4
3
93
第二次购物
6
6
162
若小明需要购买3个商品A和2个商品B,则她要花费( )
A、64元 B、65元 C、66元 D、67元7. 一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( ) A、斜坡AB的坡度是10° B、斜坡AB的坡度是tan10° C、AC=1.2tan10°米 D、AB= 米8. 如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是( )
A、斜坡AB的坡度是10° B、斜坡AB的坡度是tan10° C、AC=1.2tan10°米 D、AB= 米8. 如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是( )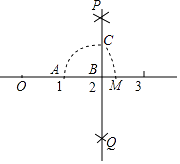 A、 B、 C、 D、9. 如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )
A、 B、 C、 D、9. 如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( )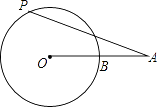 A、30° B、45° C、60° D、90°10. 在一次体育达标测试中,九年级(3)班的15名男同学的引体向上成绩如下表所示:
A、30° B、45° C、60° D、90°10. 在一次体育达标测试中,九年级(3)班的15名男同学的引体向上成绩如下表所示:成绩(个)
8
9
11
12
13
15
人数
1
2
3
4
3
2
这15名男同学引体向上成绩的中位数和众数分别是( )
A、12,13 B、12,12 C、11,12 D、3,411. 如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )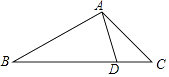 A、15 B、10 C、 D、512. 下列关于x的方程(k﹣1)x2+2kx+2=0根的情况说法正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、总有实数根13. A,B两地相距180km,新修的高速公路开通后,在A,B两地间行驶的长途客车平均车速提高了50%,而从A地到B地的时间缩短了1h.若设原来的平均车速为xkm/h,则根据题意可列方程为( )A、 ﹣ =1 B、 ﹣ =1 C、 ﹣ =1 D、 ﹣ =114. 如图,在平面直角坐标系中,直线l平行于y轴,点A在直线l上,若点P是直线l上的一个动点,且使△PAO是以OA为腰的等腰三角形,则符合条件的点P有( )
A、15 B、10 C、 D、512. 下列关于x的方程(k﹣1)x2+2kx+2=0根的情况说法正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、总有实数根13. A,B两地相距180km,新修的高速公路开通后,在A,B两地间行驶的长途客车平均车速提高了50%,而从A地到B地的时间缩短了1h.若设原来的平均车速为xkm/h,则根据题意可列方程为( )A、 ﹣ =1 B、 ﹣ =1 C、 ﹣ =1 D、 ﹣ =114. 如图,在平面直角坐标系中,直线l平行于y轴,点A在直线l上,若点P是直线l上的一个动点,且使△PAO是以OA为腰的等腰三角形,则符合条件的点P有( ) A、1个 B、2个 C、3个 D、4个15. 某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( )
A、1个 B、2个 C、3个 D、4个15. 某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( ) A、a=20 B、b=4 C、若工人甲一天获得薪金180元,则他共生产50件 D、若工人乙一天生产m(件),则他获得薪金4m元16. 如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C 的圆心坐标为(0,﹣1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是( )
A、a=20 B、b=4 C、若工人甲一天获得薪金180元,则他共生产50件 D、若工人乙一天生产m(件),则他获得薪金4m元16. 如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C 的圆心坐标为(0,﹣1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是( ) A、3 B、 C、 D、4
A、3 B、 C、 D、4二、填空题
-
17. 要使代数式 有意义,则x的取值范围是 .18. 从1、2、3、4中任取一个数作为十位上的数,再从2、3、4中任取一个数作为个位上的数,那么组成的两位数是3的倍数的概率是 .19.
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),则第4个正方形的边长为 , 第n个正方形的边长为 .

三、解答题
-
20. 先化简,再求值:( ﹣ )÷ ,其中x=tan45°+2cos60°.21. 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(5,3)、B(5,1).
 (1)、在图中标出△ABC外心D的位置,并直接写出它的坐标;(2)、判断△ABC的外接圆D与x轴、y轴的位置关系,并说明理由.22. 如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
(1)、在图中标出△ABC外心D的位置,并直接写出它的坐标;(2)、判断△ABC的外接圆D与x轴、y轴的位置关系,并说明理由.22. 如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF. (1)、求证:△ABF≌△CBE;(2)、判断△CEF的形状,并说明理由.23. 为了贯彻落实健康第一的指导思想,促进学生全面发展,国家每年都要对中学生进行一次体能测试,测试结果分“优秀”、“良好”、“及格”、“不及格”四个等级,某学校从七年级学生中随机抽取部分学生的体能测试结果进行分析,并根据收集的数据绘制了两幅不完整的统计图,请根据这两幅统计图中的信息回答下列问题
(1)、求证:△ABF≌△CBE;(2)、判断△CEF的形状,并说明理由.23. 为了贯彻落实健康第一的指导思想,促进学生全面发展,国家每年都要对中学生进行一次体能测试,测试结果分“优秀”、“良好”、“及格”、“不及格”四个等级,某学校从七年级学生中随机抽取部分学生的体能测试结果进行分析,并根据收集的数据绘制了两幅不完整的统计图,请根据这两幅统计图中的信息回答下列问题 (1)、本次抽样调查共抽取多少名学生?(2)、补全条形统计图.(3)、在扇形统计图中,求测试结果为“良好”等级所对应圆心角的度数.(4)、若该学校七年级共有600名学生,请你估计该学校七年级学生中测试结果为“不及格”等级的学生有多少名?(5)、请你对“不及格”等级的同学提一个友善的建议(一句话即可).24. 已知:等腰三角形OAB在直角坐标系中的位置如下图,点A的坐标为( ,3),点B的坐标为(﹣6,0).
(1)、本次抽样调查共抽取多少名学生?(2)、补全条形统计图.(3)、在扇形统计图中,求测试结果为“良好”等级所对应圆心角的度数.(4)、若该学校七年级共有600名学生,请你估计该学校七年级学生中测试结果为“不及格”等级的学生有多少名?(5)、请你对“不及格”等级的同学提一个友善的建议(一句话即可).24. 已知:等腰三角形OAB在直角坐标系中的位置如下图,点A的坐标为( ,3),点B的坐标为(﹣6,0). (1)、若△OAB关于y轴的轴对称图形是△OA'B',请直接写出A、B的对称点A'、B'的坐标;(2)、若将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数 的图象上,求a的值;(3)、若△OAB绕点O按逆时针方向旋转30°,此时点B恰好落在反比例函数 的图象上,求k的值.25. 两个全等的△ABC和△DEF重叠在一起,固定△ABC,将△DEF进行如下变换:(1)、如图1,△DEF沿直线CB向右平移(即点F在线段CB上移动),连接AF、AD、BD,请直接写出S△ABC与S四边形AFBD的关系;
(1)、若△OAB关于y轴的轴对称图形是△OA'B',请直接写出A、B的对称点A'、B'的坐标;(2)、若将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数 的图象上,求a的值;(3)、若△OAB绕点O按逆时针方向旋转30°,此时点B恰好落在反比例函数 的图象上,求k的值.25. 两个全等的△ABC和△DEF重叠在一起,固定△ABC,将△DEF进行如下变换:(1)、如图1,△DEF沿直线CB向右平移(即点F在线段CB上移动),连接AF、AD、BD,请直接写出S△ABC与S四边形AFBD的关系; (2)、如图2,当点F平移到线段BC的中点时,四边形AFBD是什么特殊四边形?请给出证明;
(2)、如图2,当点F平移到线段BC的中点时,四边形AFBD是什么特殊四边形?请给出证明; (3)、当点F平移到线段BC的中点时,若四边形AFBD为正方形,猜想△ABC应满足什么条件?请直接写出结论:在此条件下,将△DEF沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请在图3位置画出图形,并求出sin∠CGF的值.26. 如图1,在平面直角坐标系xOy中,点A的坐标为(0,1),取一点B(b,0),连接AB,做线段AB的垂直平分线l1 , 过点B作x轴的垂线l2 , 记l1 , l2的交点为P.
(3)、当点F平移到线段BC的中点时,若四边形AFBD为正方形,猜想△ABC应满足什么条件?请直接写出结论:在此条件下,将△DEF沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请在图3位置画出图形,并求出sin∠CGF的值.26. 如图1,在平面直角坐标系xOy中,点A的坐标为(0,1),取一点B(b,0),连接AB,做线段AB的垂直平分线l1 , 过点B作x轴的垂线l2 , 记l1 , l2的交点为P. (1)、当b=3时,在图1中补全图形(尺规作图,不写作法,保留作图痕迹);(2)、小慧多次取不同数值b,得出相应的点P,并把这些点用平滑的曲线连接起来发现:这些点P竟然在一条曲线L上!
(1)、当b=3时,在图1中补全图形(尺规作图,不写作法,保留作图痕迹);(2)、小慧多次取不同数值b,得出相应的点P,并把这些点用平滑的曲线连接起来发现:这些点P竟然在一条曲线L上!①设点P的坐标为(x,y),试求y与x之间的关系式,并指出曲线L是哪种曲线;
②设点P到x轴,y轴的距离分别是d1 , d2 , 求d1+d2的范围,当d1+d2=8时,求点P的坐标;
③将曲线L在直线y=2下方的部分沿直线y=2向上翻折,得到一条“W”形状的新曲线,若直线y=kx+3与这条“W”形状的新曲线有4个交点,直接写出k的取值范围.