江苏省泰州市兴化市2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2020-03-11 类型:期末考试
一、单选题
-
1. 下列各数是无理数的是( )A、﹣2 B、 C、0.010010001 D、π2. 2019年是中华人民共和国成立70周年,10月1日上午在天安门举行了盛大的阅兵式和群众游行,约有115000名官兵和群众参与,是我们每个中国人的骄傲.将115000用科学记数法表示为( )A、115×10 B、11.5×10 C、1.15×10 D、0.115×103. 如图所示,沿图中虚线旋转一周,能围成的几何体是下面几何体中的 ( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列各组单项式中,是同类项的一组是( )A、3x3y与3xy3 B、2ab2与-3a2b C、a2与b2 D、2xy与3 yx5. 下列图形中,线段PQ的长表示点P到直线MN的距离是( )A、
4. 下列各组单项式中,是同类项的一组是( )A、3x3y与3xy3 B、2ab2与-3a2b C、a2与b2 D、2xy与3 yx5. 下列图形中,线段PQ的长表示点P到直线MN的距离是( )A、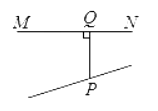 B、
B、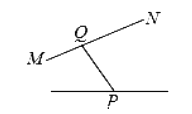 C、
C、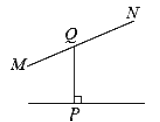 D、
D、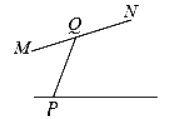 6. 如图,正方形硬纸片ABCD的边长是8,点E、F分别是AB、BC的中点,若沿图中的虚线剪开,拼成如图的一座“小房子”,则图中阴影部分的面积是( )
6. 如图,正方形硬纸片ABCD的边长是8,点E、F分别是AB、BC的中点,若沿图中的虚线剪开,拼成如图的一座“小房子”,则图中阴影部分的面积是( ) A、4 B、8 C、16 D、32
A、4 B、8 C、16 D、32二、填空题
-
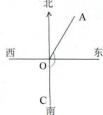
7. 的倒数是 .8. 在墙上固定一根木棒时,至少需要两根钉子,这其中所体现的“基本事实”是.9. 若a是-2x2y3的系数,c是多项式2m4n2-m7-2的次数,则ac=.10. 北京时间上午5点整,时针与分针所成的角的度数是.11. 如图,∠AOC=150°,则射线OA的方向是 .
 12. 如果代数式5a+3b的值为﹣4,则代数式2(a+b)+4(2a+b+2)的值为.13. 某款服装,一件的进价为200元,若按标价的八折销售,仍可获利20%,设这款服装每件的标价为x元,则可列方程为.14. 如图是一个正方体的展开图,把展开图折叠成正方体后,与数字3所在的面相对的面上的数字是.
12. 如果代数式5a+3b的值为﹣4,则代数式2(a+b)+4(2a+b+2)的值为.13. 某款服装,一件的进价为200元,若按标价的八折销售,仍可获利20%,设这款服装每件的标价为x元,则可列方程为.14. 如图是一个正方体的展开图,把展开图折叠成正方体后,与数字3所在的面相对的面上的数字是. 15. 一组“数值转换机”按下面的程序计算,如果输入的数是10,那么输出的结果为19,要使输出的结果为17,则输入的最小正整数是.
15. 一组“数值转换机”按下面的程序计算,如果输入的数是10,那么输出的结果为19,要使输出的结果为17,则输入的最小正整数是.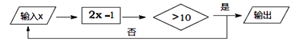 16. 如图,已知∠AOB=75°,∠COD=35°,∠COD在∠AOB的内部绕着点O旋转(OC与OA不重合,OD与OB不重合),若OE为∠AOC的角平分线.则2∠BOE-∠BOD的值为.
16. 如图,已知∠AOB=75°,∠COD=35°,∠COD在∠AOB的内部绕着点O旋转(OC与OA不重合,OD与OB不重合),若OE为∠AOC的角平分线.则2∠BOE-∠BOD的值为.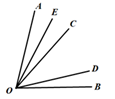
三、解答题
-
17. 计算:(1)、(2)、18. 解下列方程:(1)、 ;(2)、 .19. 已知A= ,且 ,(1)、化简:A+2B;(2)、若 ,求A+2B的值.20. 如图,在方格纸中,每个小方格的边长为1,直线AC与CD相交于点C.
 (1)、①过点E画直线EF,使EF⊥AC,垂足为F;
(1)、①过点E画直线EF,使EF⊥AC,垂足为F;②过点E画直线EG,使EG∥AC,交CD于G;
(2)、连接AE,求四边形ACDE的面积.21. 如图是一个几何体从三个方向看所得到的形状图. (1)、写出这个几何体的名称;(2)、画出它的一种表面展开图;(3)、若从正面看的高为4cm,从上面看三角形的边长都为3 cm,求这个几何体的侧面积.22. 从泰州乘“K”字头列车A、“T”字头列车B都可直达南京,已知A车的平均速度为80 km/h,B车的平均速度为A车的1.5倍,且行完全程B车所需时间比A车少40分钟.(1)、求泰州至南京的铁路里程;(2)、若两车以各自的平均速度分别从泰州、南京同时相向而行,问经过多少时间两车相距40 km?23. 如图,直线AB,CD相交于点O,OF⊥CD,OE平分∠BOC.
(1)、写出这个几何体的名称;(2)、画出它的一种表面展开图;(3)、若从正面看的高为4cm,从上面看三角形的边长都为3 cm,求这个几何体的侧面积.22. 从泰州乘“K”字头列车A、“T”字头列车B都可直达南京,已知A车的平均速度为80 km/h,B车的平均速度为A车的1.5倍,且行完全程B车所需时间比A车少40分钟.(1)、求泰州至南京的铁路里程;(2)、若两车以各自的平均速度分别从泰州、南京同时相向而行,问经过多少时间两车相距40 km?23. 如图,直线AB,CD相交于点O,OF⊥CD,OE平分∠BOC. (1)、若∠BOE=60°,求∠AOE的度数;(2)、若∠BOD:∠BOE=4:3,求∠AOE的度数.24. 用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置小立方体的个数,请解答下列问题:
(1)、若∠BOE=60°,求∠AOE的度数;(2)、若∠BOD:∠BOE=4:3,求∠AOE的度数.24. 用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置小立方体的个数,请解答下列问题: (1)、直接写出a,b,c的值;(2)、这个几何体最少有几个小立方体搭成,最多有几个小立方体搭成;(3)、当d=1,e=2,f=1时画出这个几何体的左视图.25. 已知 为整数,且满足关于x的方程(2m+1)x=3mx-1,(1)、当 时,求方程的解;(2)、该方程的解能否为3,请说明理由;(3)、当x为正整数时,请求出的m值.26. 点A、O、B、C从左向右依次在数轴上的位置如图所示,点O在原点,点A、B、C表示的数分别是a、b、c .
(1)、直接写出a,b,c的值;(2)、这个几何体最少有几个小立方体搭成,最多有几个小立方体搭成;(3)、当d=1,e=2,f=1时画出这个几何体的左视图.25. 已知 为整数,且满足关于x的方程(2m+1)x=3mx-1,(1)、当 时,求方程的解;(2)、该方程的解能否为3,请说明理由;(3)、当x为正整数时,请求出的m值.26. 点A、O、B、C从左向右依次在数轴上的位置如图所示,点O在原点,点A、B、C表示的数分别是a、b、c .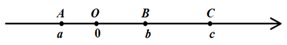 (1)、若a=﹣2,b=4,c=8,D为AB中点,F为BC中点,求DF的长.(2)、若点A到原点的距离为3,B为AC的中点.
(1)、若a=﹣2,b=4,c=8,D为AB中点,F为BC中点,求DF的长.(2)、若点A到原点的距离为3,B为AC的中点.①用b的代数式表示c;
②数轴上B、C两点之间有一动点M,点M表示的数为x,无论点M运动到何处,代数式 |x﹣c|﹣5|x﹣a|+bx+cx 的值都不变,求b的值.