湖北省孝感市云梦县2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期：2020-03-11 类型：期末考试
一、单选题
-
1. 如果水位升高5米记为+5米，那么水位下降3米应记为（ ）A、+3米 B、﹣3米 C、2米 D、﹣2米2. 第七届世界军人运动会将于2019年10月在武汉举行，届时将需要200000名城市志愿者和50000名赛会志愿者.数250000用科学记数法表示为（ ）A、2.5×104 B、25×104 C、2.5×105 D、0.25×1063. 对于多项式3x2﹣y+3x2y3+x4﹣1，下列说法正确的是（ ）A、次数为12 B、常数项为1 C、项数为5 D、最高次项为x44. 若x＝1是关于x的方程3x﹣m＝5的解，则m的值为（ ）A、2 B、﹣2 C、8 D、﹣85. 已知a＝b，下列等式不一定成立的是（ ）A、a﹣c＝b﹣c B、ac＝bc C、a2＝b2 D、 ＝16. 已知∠1的补角是它的4倍，那么∠1的度数是（ ）A、18° B、30° C、36° D、60°7. 若﹣2xm+7y4与3x4y2n是同类项，则m+n的值是（ ）A、﹣1 B、1 C、2 D、58. 如图是一个正方体的表面展开图，则原正方体中与“云”字所在的面相对的面上标的字是（ ）
A、建 B、设 C、美 D、丽9. 某车间有22名工人生产螺栓和螺母，每人每天平均生产螺栓12个或螺母20个，现有x名工人生产螺栓，其他工人生产螺母，恰好每天生产的螺栓和螺母按照1：2配套，下列方程正确的是（ ）A、12x＝20（22﹣x） B、2×12x＝20（22﹣x） C、2×20x＝12（22﹣x） D、12x＝2×20（22﹣x）10. 如图，货轮O在航行过程中，发现灯塔A在它北偏东30°的方向上，海岛B在它南偏东60°方向上.则下列结论：①∠NOA＝30°；②图中∠NOB的补角有两个，分别是∠SOB和∠EOA；③图中有4对互余的角；④货轮O在海岛B的西偏北30°的方向上.其中正确结论的个数有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 单项式﹣0.8a2h的系数是.12. 比较大小： （填“＞”“＜”或“＝”）.13. 把一个平角7等分，每一份的度数是.（精确到分）14. 在2019年的全国青少年足球超级联赛中，某队在前10场比赛中，保持连续不败，共积24分，按比赛规则，胜一场得3分，平一场得1分，那么该队共胜场.15. 已知∠AOB＝80°，∠BOC＝20°，OE平分∠AOC，则∠AOE＝.16. 用火柴棒按如图的方式搭“塔式三角形”，第一个图用了3根火柴棒，第二个图用了9根火柴棒，第三个图用了18根火柴棒，…，照这样下去，第n个图用了根火柴棒.（用含n的式子表达）
三、解答题
-
17. 计算.(1)、12×（﹣5）﹣（﹣3）÷(2)、（﹣10）3+[（﹣8）2﹣（5﹣32）×9]18. 解方程(1)、7﹣2y＝6y+3(2)、 ﹣1＝19. 如图，已知A、B、C、D四点，请按下列要求画图：（不写作法，保留作图痕迹）.
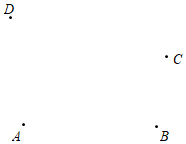
①画直线AD；
②画射线AB；③画线段BD，在BD上求作点P，使点P到A、C两点的距离之和最小.理由是 ▲ .
20. 整理一批图书，如果由一人单独做要用28h，现先安排一部分人用lh整理，随后又增加5人和他们一起又做了2h，恰好完成整理工作.假设每个人的工作效率相同，那么先安排整理的人员有多少？21. 如图，是一所住宅的建筑平面图（图中长度单位：m）.
(1)、用式子表示这所住宅的建筑面积；(2)、若a＝4，b＝6，求出这所住宅的建筑面积.22. 县城甲、乙两超市在元旦节期间分别推出如下促销方式：甲超市
乙超市
全场商品一律优惠15%
购物不超过200元，不优惠；
购物超过200元而不超过500元，一律八折；
购物超过500元，其中的500元优惠10%，超过的部分打七五折.
已知两家超市相同商品的标价都一样.
(1)、当购物总额是多少时，甲、乙两家超市实付款相同？(2)、某顾客在乙超市购物实际付款480元，试问该顾客的选择划算吗？试说明理由.23. 点C，D是半圆弧上的两个动点，在运动的过程中保持∠COD＝80°.
(1)、如图1，OM平分∠AOC，ON平分∠BOD，求∠MON的度数；(2)、如图2，若∠AOC＝x°，OM平分∠AOD，ON平分∠BOC，求∠MON的度数.24. 点A和B在数轴上对应的数分别为a和b，且（a+5）2+|b﹣4|＝0.
(1)、求线段AB的长；(2)、点C在数轴上所对应的数为x，且x是方程x﹣3＝ x﹣1的解，在线段BC上是否存在点D，使得AD+BD＝ CD？若存在，请求出点D在数轴上所对应的数，若不存在，请说明理由；(3)、如图，PO＝1，点P在AB的上方，且∠POB＝60°，点P绕着点O以30度/秒的速度在圆周上逆时针旋转一周停止，同时点Q沿线段AB自点A向点B运动，若P、Q两点能相遇，求点Q的运动速度.