湖北省黄石市大冶市2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2020-03-11 类型：期末考试

进入出卷网下载

一、单选题

1. 比﹣3大2的数是（）

A、1 B、﹣1 C、5 D、﹣5

查看试题解析
2. 下列说法中正确的是

A、 $- \frac{x y^{2}}{5}$ 的系数是－5 B、单项式x的系数为1，次数为0 C、 $- 2^{2} x y z^{2}$ 的次数是6 D、xy＋x－1是二次三项式

查看试题解析
3. 下列运算正确的是（）

A、3m+3n＝6mn B、4x³﹣3x³＝1 C、﹣xy+xy＝0 D、a⁴+a²＝a⁶

查看试题解析
4. 地球上陆地的面积约为150 000 000 km² ，把“150 000 000”用科学记数法表示为（）

A、1.5×10⁸ B、1.5×10⁷ C、1.5×10⁹ D、1.5×10⁶

查看试题解析
5. 下列选项中，移项正确的是（）

A、方程 $8 - x = 6$ 变形为 $- x = 6 + 8$ B、方程 $5 x = 4 x + 8$ 变形为 $5 x - 4 x = 8$ C、方程 $3 x = 2 x + 5$ 变形为 $3 x - 2 x = - 5$ D、方程 $3 - 2 x = x + 7$ 变形为 $x - 2 x = 7 + 3$

查看试题解析
6. 如图是一个正方体的平面展开图，把展开图折叠成正方体后，“孝”字一面相对而上的字是（）

A、包 B、容 C、大 D、气

查看试题解析
7. 把一条弯曲的公路改成直道，可以缩短路程，这其中蕴含的数学道理是（）

A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、两点之间直线最短

查看试题解析
8. 在雅礼社团年会上，各个社团大放光彩，其中话剧社52人，舞蹈社38人要外出表演，现根据演出需要，从舞蹈社中抽调了部分同学参加话剧社，使话剧社的人数恰好是舞蹈社的人数的3倍.设从舞蹈队中抽调了x人参加话剧社，可得正确的方程是（）

A、3（52﹣x）=38+x B、52+x=3（38﹣x） C、52﹣3x=38+x D、52﹣x=3（38﹣x）

查看试题解析
9. 小华在小凡的南偏东30°方位，则小凡在小华的（）方位

A、南偏东60° B、北偏西30° C、南偏东30° D、北偏西60°

查看试题解析
10. 下列说法：①若|a|＝﹣b，|b|＝b，则a＝b＝0；②若﹣a不是正数，则a为非负数；③|﹣a²|＝（﹣a）²；④若 $\frac{a}{| a |} + \frac{b}{| b |} = 0$ ，则 $\frac{a b}{| a b |} = - 1$ ；⑤平面内n条直线两两相交，最多 $\frac{n (n + 1)}{2}$ 个交点.其中正确的结论有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 一只蚂蚁从数轴上一点 A出发，爬了7 个单位长度到了+1，则点 A 所表示的数是

查看试题解析
12. 若﹣5a^m+1b²与 $\frac{1}{3}$ aⁿbⁿ^﹣¹是同类项，则m﹣n的值为.

查看试题解析
13. 一文具店在某一时间以每件30元的价格卖出两个笔袋，其中一个盈利25%，另一个亏损25%.卖这两个笔袋总的盈亏情况是元（填盈利或亏损多少）

查看试题解析
14. 在一条直线上取A，B，C三点，使得AB=5cm，BC=3cm．如果点D是线段AC的中点，那么线段DB的长度是cm．

查看试题解析
15. 若∠A与∠B互为补角，并且∠B的一半比∠A小30°，则∠B为°.

查看试题解析
16. 古希腊数学家把数1，3，6，10，15，21，……叫三角形数，它有一定的规律性，若把第一个三角形数记为a₁ ，第二个三角形数记为a₂…第n个三角形数记为a_n ，则a_n＝.

查看试题解析

三、解答题

17. 计算： $(\frac{3}{4} - \frac{1}{6} + \frac{3}{8}) \times (- 24) + {(- 3)}^{2} \div 12$

查看试题解析
18. 解方程： $\frac{3 x + 2}{2} - 1 = \frac{2 x + 1}{4} - \frac{2 x + 1}{5}$

查看试题解析
19. 先化简，再求值： $5 (3 a^{2} b - a b^{2}) - 4 (- a b^{2} + 3 a^{2} b)$ ，其中 $a = \frac{1}{2}$ ， $b = - \frac{1}{3}$ .

查看试题解析
20. 已知a、b、c在数轴上对应的点如图所示，

(1)、化简：2|b﹣c|﹣|b+c|+|a﹣c|﹣|a﹣b|；

(2)、若（c+4）²与|a+c+10|互为相反数，且b＝|a﹣c|，求（1）中式子的值.

查看试题解析
21. 我们规定，若关于x的一元一次方程ax=b的解为b﹣a，则称该方程为“差解方程”，例如：2x=4的解为2，且2=4﹣2，则该方程2x=4是差解方程．
请根据上边规定解答下列问题：

(1)、判断3x=4.5是否是差解方程；

(2)、若关于x的一元一次方程6x=m+2是差解方程，求m的值．

查看试题解析
22. 如图，线段AB＝8cm，C是线段AB上一点，AC＝3.2cm，M是AB的中点，N是AC的中点.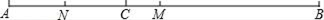

(1)、求线段CM的长；

(2)、求线段MN的长.

查看试题解析
23. 如图，点O在直线AB上，∠AOC与∠COD互补，OE平分∠AOC.

(1)、若∠BOC＝40°，则∠DOE的度数为；

(2)、若∠DOE＝48°，求∠BOD的度数.

查看试题解析

24. 为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，某市自来水收费的价目表如下（水费按月结算，m³表示立方米）

价目表
每月用水量	价格
不超过6m³的部分	3元/m³
超过6m³不超过10m³的部分	5元/m³
超过10m³的部分	8元/m³

根据上表的内容解答下列问题：

(1)、若小亮家1月份用水4m³ ，则应交水费元；（直接写出答案，不写过程）；

(2)、若小亮家2月份用水am³（其中6＜a≤10），求小明家2月份应交水费多少元？（用含a的式子表示，写出过程并化简）；

(3)、若小亮家3月份交水费62元，求小亮家3月份的用水量是多少m³.

查看试题解析

25. 已知M＝（a＋24）x³﹣10x²＋10x＋5是关于x的二次多项式，且二次项系数和一次项系数分别为b和c，在数轴上A、B、C三点所对应的数分别是a、b、c.

(1)、则a＝， b＝， c＝.

(2)、有一动点P从点A出发，以每秒4个单位的速度向右运动，多少秒后，P到A、B、C的距离和为40个单位？

(3)、在（2）的条件下，当点P移动到点B时立即掉头，速度不变，同时点T和点Q分别从点A和点C出发，向左运动，点T的速度1个单位/秒，点Q的速度5个单位/秒，设点P、Q、T所对应的数分别是x_P、x_Q、x_T ，点Q出发的时间为t，当 $\frac{14}{3}$ ＜t＜ $\frac{17}{2}$ 时，求2|x_P﹣x_T|＋|x_T﹣x_Q|＋2|x_Q﹣x_P|的值.

查看试题解析