河南省新乡市长垣市2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2020-03-11 类型：期末考试

进入出卷网下载

一、单选题

1. $- \frac{1}{6}$ 的相反数是（）

A、 $- 6$ B、6 C、 $- \frac{1}{6}$ D、 $\frac{1}{6}$

查看试题解析
2. 随着我国金融科技不断发展，网络消费、网上购物已成为人们生活不可或缺的一部分，今年“双十一”天猫成交额高达2684亿元.将数据“2684亿”用科学记数法表示（）

A、 $2.684 \times 10^{3}$ B、 $2.684 \times 10^{11}$ C、 $2.684 \times 10^{12}$ D、 $2.684 \times 10^{7}$

查看试题解析
3. 下列各组中的两个单项式，属于同类项的一组是（）

A、 $3 a^{2} b$ 与 $3 a b^{2}$ B、 $2 x$ 与 $\frac{2}{x}$ C、 $3^{2}$ 与 $a^{2}$ D、 $4$ 与 $- \frac{1}{2}$

查看试题解析
4. 下列等式变形正确的是（）

A、由a=b，得 $\frac{a}{- 3}$ = $\frac{b}{- 3}$ B、由﹣3x=﹣3y，得x=﹣y C、由 $\frac{x}{4}$ =1，得x= $\frac{1}{4}$ D、由x=y，得 $\frac{x}{a}$ = $\frac{y}{a}$

查看试题解析
5. 高速公路的建设带动我国经济的快速发展.在高速公路的建设中，通常要从大山中开挖隧道穿过，把道路取直，以缩短路程.这样做包含的数学道理是（）

A、两点确定一条直线 B、两点之间，线段最短 C、两条直线相交，只有一个交点 D、直线是向两个方向无限延伸的

查看试题解析
6. 有理数a，b在数轴上的位置如图，则下列各式不成立的是（）

A、a+b＜0 B、a﹣b＞0 C、ab＞0 D、|b|＞a

查看试题解析
7. 如图，是小明同学在数学实践课上，所设计的正方体盒子的平面展开图，每个面上都有一个汉字，请你判断，正方体盒子上与“善”字相对的面上的字是（）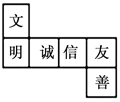

A、文 B、明 C、诚 D、信

查看试题解析
8. 若 $x - 3 y = 4$ ，则 $1 + 3 y - x$ 的值是（）

A、 $- 3$ B、5 C、3 D、 $- 5$

查看试题解析
9. 已知线段AB=3cm,点C在线段AB所在的直线上，且BC=1cm,则线段AC的长度为（）

A、4cm B、2cm C、2cm或4cm D、3cm

查看试题解析
10. 《九章算术》中有一道阐述“盈不足术”的问题，原文如下：今有人共买物，人出八，盈三；人出七，不足四．问人数，物价各几何？译文为：现有一些人共同买一个物品，每人出8元，还盈余3元；每人出7元，则还差4元，问共有多少人？这个物品的价格是多少？设这个物品的价格是x元，则可列方程为（）

A、8x+3=7x+4 B、8x﹣3=7x+4 C、 $\frac{x - 3}{8} = \frac{x + 4}{7}$ D、 $\frac{x + 3}{8} = \frac{x - 4}{7}$

查看试题解析

二、填空题

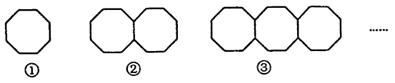
11. 我县2019年1月的一天早晨的气温是﹣11℃，中午的气温比早晨上升了8℃，中午的气温是℃.

查看试题解析
12. 在数轴上，点A表示数－4，距A点3个单位长度的点表示的数是.

查看试题解析
13. 已知∠α+∠β=90°，且∠α=35°41′，则∠β=.

查看试题解析
14. 一根铁丝正好围成一个长方形，一边长为2a+b，另一边比它长3a﹣b，则长方形的周长为.

查看试题解析
15. 下列图案是用长度相同的火柴棒按一定规律拼搭而成，图案 $①$ 需8根火材棒，图案 $②$ 需15根火柴棒， $\dots \dots$ ，按此规律，图案 $ⓝ$ 需根火材棒.

查看试题解析

三、解答题

16. 计算：

(1)、 $| - 2 \frac{1}{4} | - (- \frac{3}{4}) + 1 - | 1 - \frac{1}{2} |$ ；

(2)、 $- 3^{2} - [8 \div {(- 2)}^{3} - 1] + 3 \div 2 \times \frac{1}{2}$ ；

查看试题解析
17. 解方程：

(1)、3x﹣7（x﹣1）=3﹣2（x+3）

(2)、 $\frac{2 x - 1}{3} - \frac{5 - x}{6}$ =﹣1.

查看试题解析
18. 化简求值： $- a^{2} b + 3 (3 a b^{2} - a^{2} b) - 2 (2 a b^{2} - a^{2} b)$ ，其中 $| a - 1 | + {(b + 2)}^{2} = 0$ .

查看试题解析
19. 如图，已知A、O、B三点共线，∠AOD=42°，∠COB=90°.

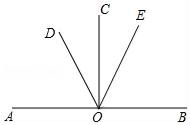(1)、求∠BOD的度数；

(2)、若OE平分∠BOD，求∠COE的度数.

查看试题解析
20. 世界杯比赛中，根据场上攻守形势，守门员会在门前来回跑动，如果以球门线为基准，向前跑记作正数，返回则记作负数，一段时间内，某守门员的跑动情况记录如下（单位： $m$ ）： $+ 10$ ， $- 2$ ， $+ 5$ ， $- 6$ ， $+ 12$ ， $- 9$ ， $+ 4$ ， $- 14$ .（假定开始计时时，守门员正好在球门线上）

(1)、守门员最后是否回到球门线上？

(2)、守门员在这段时间内共跑了多少米？

(3)、如果守门员离开球门线的距离超过10米（不包括10米），则对方球员挑射极可能造成破门.请问在这一时间段内，对方球员有几次挑射破门的机会？

查看试题解析

21. 已知

y_{1} = - x + 4

，

y_{2} = 2 x - 2

(1)、当

x

为何值时，

y_{1} = y_{2}

；

(2)、当

x

为何值时，

y_{1}

的值比

y_{2}

的值的

\frac{1}{2}

大1；

(3)、填表，

$x$	$- 3$	$- 2$	$- 1$	0	1	2	3	4
$y_{1}$
$y_{2}$

(4)、根据所填表格，回答问题：随着

x

值的增大，

y_{1}

的值逐渐；

y_{2}

的值逐渐.

查看试题解析

22. 如图，C为线段AB上一点，点D为BC的中点，且AB＝18cm，AC＝4CD．

(1)、图中共有条线段；

(2)、求AC的长；

(3)、若点E在直线AB上，且EA＝2cm，求BE的长．

查看试题解析
23. 某学校准备印刷一批证书，现有两个印刷厂可供选择：
甲厂收费方式：收制版费1000元，每本印刷费0.5元；

乙厂收费方式：不超过2000本时，每本收印刷费1.5元；超过2000本超过部分每本收印刷费0.25元，若该校印制证书x本．

(1)、若x 不超过2000时，甲厂的收费为元，乙厂的收费为元；

(2)、若x 超过2000时，甲厂的收费为元，乙厂的收费为元

(3)、当印制证书8000本时应该选择哪个印刷厂更节省费用？节省了多少？

(4)、请问印刷多少本证书时，甲乙两厂收费相同？

查看试题解析