江苏省连云港市赣榆区2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-03-11 类型：期末考试

进入出卷网下载

一、单选题

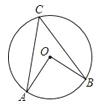
1. 若关于x的方程x²+6x+k=0有两个相等的实数根，则k的值为（）

A、0 B、-9 C、9 D、-6

查看试题解析
2. 为了解当地气温变化情况，某研究小组记录了冬天连续4天的最高气温，结果如下（单位： $° C$ ）：－1，－3，－1，5.下列结论错误的是（）

A、平均数是0 B、中位数是－1 C、众数是－1 D、方差是6

查看试题解析
3. 一个不透明的口袋中有4个完全相同的小球，分别将它们标上1，2，3，4，随机摸出标号为3的小球的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{3}{4}$

查看试题解析
4.
已知：如图，OA，OB是⊙O的两条半径，且OA⊥OB，点C在⊙O上，则∠ACB的度数为（　　）

A、45° B、35° C、25° D、20°

查看试题解析
5. 九江某快递公司随着网络的发展，业务增长迅速，完成快递件数从六月份的10万件增长到八月份的12.1万件.假定每月增长率相同，设为x.则可列方程为（）

A、 $10 x + x^{2} = 12.1$ B、 $10 (x + 1) = 12.1$ C、 $10 {(1 + x)}^{2} ＝ 12.1$ D、 $10 + 10 (1 + x) = 12.1$

查看试题解析
6. 对于抛物线 $y = {(x - 2)}^{2} - 3$ ，下列结论错误的是（）

A、抛物线的开口向上 B、对称轴是直线 $x = 2$ C、抛物线不经过第三象限 D、当 $x > 3$ 时， $y$ 随 $x$ 的增大而减小

查看试题解析
7. 如图，在△ABC中，DE∥BC， $\frac{A D}{D B} = \frac{1}{2}$ ，则下列结论中正确的是（）

A、 $\frac{A E}{A C} = \frac{1}{2}$ B、 $\frac{D E}{B C} = \frac{1}{2}$ C、 $\frac{△ A D E 的周长}{△ A B C 的周长} = \frac{1}{3}$ D、 $\frac{△ A D E 的面积}{△ A B C 的面积} = \frac{1}{3}$

查看试题解析
8. 在平面直角坐标系中，已知点 $A (- \frac{1}{2} ， 1)$ 和 $B (1 ， 4)$ 都在直线 $y = 2 x + 2$ 上，若抛物线 $y = a x^{2} - x + 1 (a \neq 0)$ 与线段 $A B$ 有两个不同的交点，则 $a$ 的取值范围是（）

A、 $a ⩾ 4$ 或 $a ⩽ - 2$ B、 $- \frac{9}{4} < a ⩽ - 2$ C、 $- 2 ⩽ a ⩽ 4$ D、 $- \frac{9}{4} < a ⩽ - 2$ 或 $a ⩾ 4$

查看试题解析

二、填空题

9. 小刘和小李参加射击训练，各射击10次的平均成绩相同，如果他们射击成绩的方差分别是S_小刘²＝0.6，S_小李²＝1.4，那么两人中射击成绩比较稳定的是；

查看试题解析
10. 一个圆锥的母线长为5cm，底面半径为2cm，那么这个圆锥的侧面积为cm².

查看试题解析
11. 若点 $M (- 3, y_{1})$ ， $N (- 1, y_{2})$ ， $P (4, y_{3})$ 在抛物线 $y = - x^{2} + 2 x + m$ 上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 大小顺序为.（用“<”号连接）

查看试题解析
12. 已知线段AB＝10cm，点P是线段AB的黄金分割点，且PA＞PB，则PA＝cm.（精确到0.1）

查看试题解析
13. 已知学校航模组设计制作的火箭模型的升空高度h（m）与飞行时间t（s）满足函数表达式h=﹣t²+24t+1.则火箭升空到最高点需要的时间为.

查看试题解析
14. 已知点G是 $△ A B C$ 的重心，过点G作MN//BC分别交边AB、AC于点M、N，那么 $\frac{S_{△ A M N}}{S_{△ A B C}} =$

查看试题解析
15. 当 $0 ⩽ x ⩽ 4$ 时，直线 $y = t$ 与抛物线 $y = x^{2} - 2 x - 3$ 有交点，则 $t$ 的取值范围是.

查看试题解析
16. 如图，在平面直角坐标系中，已知 $A (0 ， 6)$ ， $B (2 ， 0)$ ， $C (6 ， 0)$ ， $D$ 为线段 $B C$ 上的动点，以 $A D$ 为边向右侧作正方形 $A D E F$ ，连接 $C F$ 交 $D E$ 于点 $P$ ，则 $C P$ 的最大值.

查看试题解析

三、解答题

17.

(1)、解方程 $3 {(x - 2)}^{2} = 4 (x - 2)$ ；

(2)、已知 $a : b : c = 3 : 2 : 4$ .求 $\frac{a - 3 b + 4 c}{2 a + b - c}$ 的值.

查看试题解析
18. 甲、乙两台机床同时加工直径为 $10 mm$ 的同种规格零件，为了检查两台机床加工零件的稳定性，质检员从两台机床的产品中各抽取 $5$ 件进行检测，结果如下（单位： $mm$ ）：

甲

$10$

$9.8$

$10$

$10.2$

$10$

乙

$9.9$

$10$

$10$

$10.1$

$10$

(1)、分别求出这两台机床所加工零件直径的平均数和方差；

(2)、根据所学的统计知识，你认为哪一台机床生产零件的稳定性更好一些，说明理由.

查看试题解析
19. 如图，在4×4的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.

(1)、填空：∠ABC=°，BC=；

(2)、判断△ABC与△DEF是否相似，并证明你的结论.

查看试题解析
20. 已知二次函数 $y = - x^{2} + 4 x$ .

(1)、在给定的直角坐标系中，画出这个函数的图象；

(2)、根据图像，写出当 $y < 0$ 时， $x$ 的取值范围；

(3)、若将此图像沿 $x$ 轴向左平移3个单位，向下移动2个单位，请写出平移后图像所对应的函数表达式.

查看试题解析
21. 如图，四边形 $A B C D$ 是 $⊙ O$ 的内接四边形， $\overset{⌢}{A D} = \overset{⌢}{B D}$ ， $A C$ 为直径， $D E ⊥ B C$ ，垂足为 $E$ .

(1)、求证： $C D$ 平分 $∠ A C E$ ；

(2)、若 $A C = 8$ ， $C E = 3$ ，求 $C D$ 的长.

查看试题解析
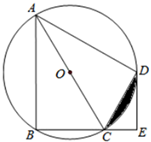22. 元旦汇演，小明同学演出，他准备的道具是：甲、乙、丙三个袋中均装有三张除所写汉字外完全相同的卡片，三张卡片上分别标有的三个字为“中”“国”、“梦”，

(1)、小明在甲袋中随机取出一张卡片，求卡片上字是“梦”的概率；

(2)、小明随机从甲、乙、丙三个袋中各取出一张，用画树状图或列表格的方法，求取出的三张字卡能够组成“中国梦”的概率.

查看试题解析
23. 一块直角三角形木板的一条直角边 $A B$ 长为3米，面积为6平方米，要把它加工成如图所示的正方形桌面，某同学的加工方法如图所示，请你用学过的知识求出该同学加工的正方形边长（加工损耗忽略不计，计算结果中的分数可保留）

查看试题解析
24. 超市销售某种儿童玩具，如果每件利润为40元（市场管理部门规定，该种玩具每件利润不能超过60元），每天可售出50件.根据市场调查发现，销售单价每增加2元，每天销售量会减少1件.设销售单价增加 $x$ 元，每天售出 $y$ 件.

(1)、请写出 $y$ 与 $x$ 之间的函数表达式；

(2)、当 $x$ 为多少时，超市每天销售这种玩具可获利润2250元？

(3)、设超市每天销售这种玩具可获利 $w$ 元，当 $x$ 为多少时 $w$ 最大，最大值是多少？

查看试题解析
25. 如图， $Rt Δ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 6 cm$ ， $B C = 8 cm$ ，动点 $P$ 从点 $B$ 出发，在 $B A$ 边上以每秒 $3 cm$ 的速度向点 $A$ 匀速运动，同时动点 $Q$ 从点 $C$ 出发，在 $C B$ 边上以每秒 $2 cm$ 的速度向点 $B$ 匀速运动，运动时间为 $t$ 秒（ $0 < t < 2$ ），连接 $P Q$ .

(1)、若 $Δ B P Q$ 与 $Δ A B C$ 相似，求 $t$ 的值；

(2)、连接 $A Q$ ， $C P$ ，若 $A Q ⊥ C P$ ，求 $t$ 的值.

查看试题解析
26. 如图，在平面直角坐标系中，已知抛物线 $y = a x^{2} + b x + 2 (a \neq 0)$ 与 $x$ 轴交于 $A (- 1 ， 0)$ ， $B (3 ， 0)$ 两点，与 $y$ 轴交于点 $C$ ，连接 $B C$ .

(1)、求该抛物线的函数表达式；

(2)、若点 $N$ 为抛物线对称轴上一点，抛物线上是否存在点 $M$ ，使得以 $B$ ， $C$ ， $M$ ， $N$ 为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点 $M$ 的坐标；若不存在，请说明理由；

(3)、点 $P$ 是直线 $B C$ 上方抛物线上的点，若 $∠ P C B = ∠ B C O$ ，求出 $P$ 点的到 $y$ 轴的距离.

查看试题解析

甲	$10$	$9.8$	$10$	$10.2$	$10$
乙	$9.9$	$10$	$10$	$10.1$	$10$