河南省新乡市卫辉市2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-03-11 类型:期末考试
一、单选题
-
1. 下列各数中,最小的数是( )A、-2020 B、2020 C、 D、2. 共享单车的投放使用为人们的工作和生活带来了极大的便利,不仅有效缓解了出行“最后一公里”问题,而且经济环保,据相关部门2018年11月统计数据显示,郑州市互联网租赁自行车累计投放超过49万辆,将49万用科学记数法表示正确的是( )A、4.9×104 B、4.9×105 C、0.49×104 D、49×1043. 如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 已知点P(3a﹣3,1﹣2a)关于x轴的对称点在第三象限,则a的取值范围在数轴上表示正确的是( )A、
4. 已知点P(3a﹣3,1﹣2a)关于x轴的对称点在第三象限,则a的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列说法中,正确的是( )A、为检测市场上正在销售的酸奶质量,应该采用全面调查的方式 B、在连续5次的数学测试中,两名同学的平均分相同,方差较大的同学数学成绩更稳定 C、小强班上有3个同学都是16岁,因此小强认为他们班学生年龄的众数是16岁 D、给定一组数据,则这组数据的中位数一定只有一个6. 若关于x的一元二次方程 有实数根,则k的取值范围在数轴上表示正确的是( )A、
5. 下列说法中,正确的是( )A、为检测市场上正在销售的酸奶质量,应该采用全面调查的方式 B、在连续5次的数学测试中,两名同学的平均分相同,方差较大的同学数学成绩更稳定 C、小强班上有3个同学都是16岁,因此小强认为他们班学生年龄的众数是16岁 D、给定一组数据,则这组数据的中位数一定只有一个6. 若关于x的一元二次方程 有实数根,则k的取值范围在数轴上表示正确的是( )A、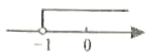 B、
B、 C、
C、 D、
D、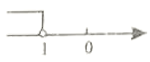 7. 从九年级一班3名优秀干部和九二班2名优秀干部中随机抽取两名学生担任升旗手,则抽取的两名学生刚好一个班的概率为( )A、 B、 C、 D、8. 某校团委准备举办学生绘画展览,为美化画面,在长8 dm、宽为5 dm的矩形内画面四周镶上宽度相等的彩纸,并使彩纸的面积等于22 (如图),若设彩纸的宽度为x dm,则可得方程式为( )
7. 从九年级一班3名优秀干部和九二班2名优秀干部中随机抽取两名学生担任升旗手,则抽取的两名学生刚好一个班的概率为( )A、 B、 C、 D、8. 某校团委准备举办学生绘画展览,为美化画面,在长8 dm、宽为5 dm的矩形内画面四周镶上宽度相等的彩纸,并使彩纸的面积等于22 (如图),若设彩纸的宽度为x dm,则可得方程式为( )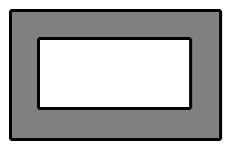 A、 B、 C、 D、9. 如图,小明为了测量高楼MN的高度,在离N点20米的A处放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度(精确到0.1米)约是( )
A、 B、 C、 D、9. 如图,小明为了测量高楼MN的高度,在离N点20米的A处放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度(精确到0.1米)约是( ) A、18.75米 B、18.8米 C、21.3米 D、19米10. 如图一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1 , 它与x轴交于点O和A1;将C1绕A1旋转180°得到C2 , 交x轴于A2;将C2绕A2旋转180°得到C3 , 交x轴于A3 , 如此进行下去,直至得到C10 , 若点P(28,m)在第10段抛物线C10上,则m的值为( )
A、18.75米 B、18.8米 C、21.3米 D、19米10. 如图一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1 , 它与x轴交于点O和A1;将C1绕A1旋转180°得到C2 , 交x轴于A2;将C2绕A2旋转180°得到C3 , 交x轴于A3 , 如此进行下去,直至得到C10 , 若点P(28,m)在第10段抛物线C10上,则m的值为( ) A、1 B、﹣1 C、2 D、﹣2
A、1 B、﹣1 C、2 D、﹣2二、填空题
-
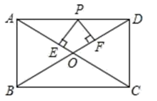
11. 16的平方根是 ,9的立方根是 .12. 一个不透明布袋里共有5个球(只有颜色不同),其中3个是黑球,2个是白球,从中随机摸出一个球,记下颜色后放回、搅匀,再随机摸出一个球,则两次摸出的球是一黑一白的概率是.13. 已知点 , , 都在二次函数 的图像上,则 的大小关系是.14. 如图所示,在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,求PE+PF的值为.
 15. 如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为 .
15. 如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为 .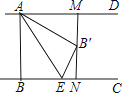
三、解答题
-
16. 先化简,再求值: ,其中a是方程a(a+1)=0的解.17. 全民学习、终身学习是学习型社会的核心内容,努力建设学习型家庭也是一个重要组成部分.为了解“学习型家庭”情况,对部分家庭五月份的平均每天看书学习时间进行了一次抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
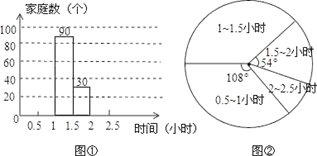 (1)、本次抽样调查了个家庭;(2)、将图①中的条形图补充完整;(3)、学习时间在2~2.5小时的部分对应的扇形圆心角的度数是度;(4)、若该社区有家庭有3000个,请你估计该社区学习时间不少于1小时的约有多少个家庭?18. 已知关于x的一元二次方程(x-3)(x-2)=|m|.(1)、求证:对于任意实数m,方程总有两个不等的实数根;(2)、若方程的一个根是1,求m的值及方程的另一个根.19. 如题,AB是⊙O的直径,在圆上取点C,延长BC到D,使BC=CD,连接AD交于⊙O于点E,过点C作CF⊥AD,垂足为F.
(1)、本次抽样调查了个家庭;(2)、将图①中的条形图补充完整;(3)、学习时间在2~2.5小时的部分对应的扇形圆心角的度数是度;(4)、若该社区有家庭有3000个,请你估计该社区学习时间不少于1小时的约有多少个家庭?18. 已知关于x的一元二次方程(x-3)(x-2)=|m|.(1)、求证:对于任意实数m,方程总有两个不等的实数根;(2)、若方程的一个根是1,求m的值及方程的另一个根.19. 如题,AB是⊙O的直径,在圆上取点C,延长BC到D,使BC=CD,连接AD交于⊙O于点E,过点C作CF⊥AD,垂足为F. (1)、求证:CF是⊙O的切线.(2)、若 , ,求CF的长.20. 被誉为“中原第一高楼”的郑州会展宾馆(俗称“大玉米”)坐落在风景如画的如意湖畔,是来郑州观光的游客留影的最佳景点,学完了三角函数知识后,刘明和王华同学决定用自己学到的知识测量“大玉米”的高度他们制订了测量方案,并利用课余时间完成了实地测量,测量项目及结果如下表
(1)、求证:CF是⊙O的切线.(2)、若 , ,求CF的长.20. 被誉为“中原第一高楼”的郑州会展宾馆(俗称“大玉米”)坐落在风景如画的如意湖畔,是来郑州观光的游客留影的最佳景点,学完了三角函数知识后,刘明和王华同学决定用自己学到的知识测量“大玉米”的高度他们制订了测量方案,并利用课余时间完成了实地测量,测量项目及结果如下表
请你帮助该小组根据上表中的测量数据,求出郑州会展宾馆的高度.
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果保留整数)
21. 某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.(1)、求y与x的函数关系式并直接写出自变量x的取值范围;(2)、每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?22. 问题发现:如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M,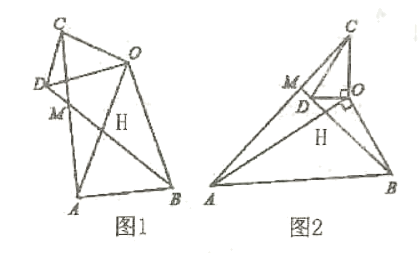 (1)、填空: 的值为; ∠AMB的度数为 ,(2)、类比探究,如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M,请判断 的值及∠AMB的度数,并说明理由:23. 如图,直线 与x轴交于点A(3,0),与y轴交于点B,抛物线 经过点A,B.
(1)、填空: 的值为; ∠AMB的度数为 ,(2)、类比探究,如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M,请判断 的值及∠AMB的度数,并说明理由:23. 如图,直线 与x轴交于点A(3,0),与y轴交于点B,抛物线 经过点A,B. (1)、求点B的坐标和抛物线的解析式;(2)、设点M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
(1)、求点B的坐标和抛物线的解析式;(2)、设点M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.①求PN的最大值;
②若以B,P,N为顶点的三角形与△APM相似,请直接写出点M的坐标.