河南省南阳市镇平县2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-03-11 类型:期末考试
一、单选题
-
1. 下列事件中,不确定事件是( )A、在空气中,汽油遇上火就燃烧 B、用力向上抛石头,石头落地 C、下星期六是晴天 D、任何数和零相乘,结果仍为零2. 下列各式计算正确的是( )A、 B、 C、 D、3. 若二次函数 的图象经过原点,则 的值必为( )
A、0或2 B、0 C、2 D、无法确定4. 关于抛物线y=x2﹣2x+1,下列说法错误的是( )A、开口向上 B、与x轴有一个交点 C、对称轴是直线x=1 D、当x>1时,y随x的增大而减小5. 一个口袋中放着若干个红球和白球,这两种球除了颜色以外没有其他区别,袋中的球已经搅匀,蒙上眼睛从口袋中取出一个球,取出红球的概率是 ,如果袋中的白球有15个,那么袋中的红球有( )A、2个 B、3个 C、4个 D、6个6. 今年我市计划扩大城区绿地面积,现有一块长方形绿地,它的短边长为60m,若将短边增长到长边相等(长边不变),使扩大后的棣地的形状是正方形,则扩大后的绿地面积比原来增加1600 ,设扩大后的正方形绿地边长为xm,下面所列方程正确的是( )A、x(x-60)=1600 B、x(x+60)=1600 C、60(x+60)=1600 D、60(x-60)=16007. 如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是( ) A、 B、 C、 D、8. 如图,正方形ABCD的边长为2,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为( )
A、 B、 C、 D、8. 如图,正方形ABCD的边长为2,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为( )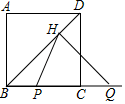 A、
A、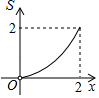 B、
B、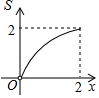 C、
C、 D、
D、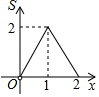 9. 如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB′C′D′的位置,B′C′与CD相交于点M,则M的坐标为( )
9. 如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB′C′D′的位置,B′C′与CD相交于点M,则M的坐标为( )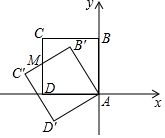 A、(1, ) B、(﹣1, ) C、(1, ) D、(﹣1, )10. 小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为300 , 同一时 刻,一根长为l米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )
A、(1, ) B、(﹣1, ) C、(1, ) D、(﹣1, )10. 小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为300 , 同一时 刻,一根长为l米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )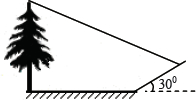 A、 米 B、12米 C、 米 D、10米
A、 米 B、12米 C、 米 D、10米二、填空题
-
11. 已知 , ,则 的值为.12. 某种药品原来售价100元,连续两次降价后售价为81元,若每次下降的百分率相同,则这个百分率是 .13. 如图,长4 m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后楼梯AC长为m.
 14. 二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:
14. 二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:x
…
﹣3
﹣2
﹣1
0
1
…
y
…
﹣3
﹣2
﹣3
﹣6
﹣11
…
则该函数图象的对称轴是
15. 如图,矩形纸片ABCD中,AB=3,AD=5,点P是边BC上的动点,现将纸片折叠使点A与点P重合,折痕与矩形边的交点分别为E,F,要使折痕始终与边AB,AD有交点,BP的取值范围是.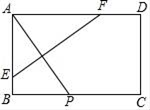
三、解答题
-
16. 先化简( ﹣1)÷ ,再求值,其中x是一元二次方程x2﹣3x+2=0的两根.17. 关于 的一元二次方程 有两个不相等的实数根.(1)、求 的取值范围;(2)、当 取满足条件的最大整数时,求方程的根.18. 已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
x
…
﹣1
0
1
2
4
…
y
…
10
1
﹣2
1
25
…
(1)、求这个二次函数的解析式;(2)、写出这个二次函数图象的开口方向、对称轴和顶点坐标.19. 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P, 在近岸取点Q和S, 使点P、Q、S共线且直线PS与河垂直,接着再过点S且与PS垂直的直线a上选择适当的点T, 确定PT与过点Q且垂直PS的直线b的交点R. 如果测得QS=45m,ST=90m,QR=60m, 求河的宽度PQ.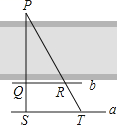 20. 学校选学生会正副主席,需要从甲班的2名男生1名女生(男生用A,B表示,女生用a表示)和乙班的1名男生1名女生(男生用C表示,女生用b表示)共5人中随机选出2名同学.(1)、用树状图或列表法列出所有可能情形;(2)、求2名同学来自不同班级的概率;(3)、求2名同学恰好1男1女的概率.21.
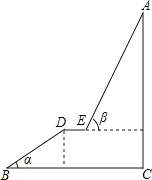
20. 学校选学生会正副主席,需要从甲班的2名男生1名女生(男生用A,B表示,女生用a表示)和乙班的1名男生1名女生(男生用C表示,女生用b表示)共5人中随机选出2名同学.(1)、用树状图或列表法列出所有可能情形;(2)、求2名同学来自不同班级的概率;(3)、求2名同学恰好1男1女的概率.21.如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
 22. 如图1,在Rt△ABC中,∠C=90°,AC=BC=2,点D、E分别在边AC、AB上,AD=DE= AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
22. 如图1,在Rt△ABC中,∠C=90°,AC=BC=2,点D、E分别在边AC、AB上,AD=DE= AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.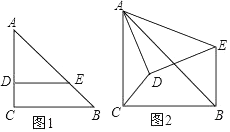 (1)、问题发现
(1)、问题发现①当θ=0°时, =;
②当θ=180°时, = .
(2)、拓展探究试判断:当0°≤θ<360°时, 的大小有无变化?请仅就图2的情形给出证明;
(3)、问题解决①在旋转过程中,BE的最大值为;
②当△ADE旋转至B、D、E三点共线时,线段CD的长为 .
23. 如图,直线 与x轴交于点A(3,0),与y轴交于点B,抛物线 经过点A,B. (1)、求点B的坐标和抛物线的解析式;(2)、设点M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
(1)、求点B的坐标和抛物线的解析式;(2)、设点M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.①求PN的最大值;
②若以B,P,N为顶点的三角形与△APM相似,请直接写出点M的坐标.