河南省南阳市邓州市2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-03-11 类型：期末考试

进入出卷网下载

一、单选题

1. 若二次根式 $\sqrt{x - 1}$ 有意义，则 $x$ 的取值范围是（）

A、 $x > 1$ B、 $x ⩾ 1$ C、 $x ⩽ 1$ D、 $x < 1$

查看试题解析
2. 方程（x-5）(x+2)=0的解是（）

A、x＝5 B、x＝－2 C、x₁＝－5，x₂＝2 D、x₁＝5，x₂＝-2

查看试题解析
3. 如图，在4×4的正方形网格中，是相似三角形的是（）

A、①③ B、①② C、②③ D、②④

查看试题解析
4. 如图，在平面直角坐标系中，直线OA过点（2，1），则cosα的值是（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{1}{2}$ C、 $\frac{2 \sqrt{5}}{5}$ D、2

查看试题解析
5. 如图，某风景区为了方便游人参观，计划从主峰A处架设一条缆车线路到另一山峰C处，若在A处测得C处的俯角为30°，两山峰的底部BD相距900米，则缆车线路AC的长为（）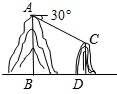

A、300 $\sqrt{3}$ 米 B、600 $\sqrt{3}$ 米 C、900 $\sqrt{3}$ 米 D、1800米

查看试题解析
6. 某商店今年10月份的销售额是2万元，12月份的销售额是2.88万元，从10月份到12月份，该商店销售额平均每月的增长率为（）

A、44% B、22% C、20% D、10%

查看试题解析
7. 从九（1）班2名优秀班干部和九（2）班2名优秀班干部中，随机选取两名学生担任升旗手，则选取的两名升旗手不是同一个班的概率为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
8. 如图，在Rt△ABC中，∠C＝90°，AD＝BD，CE＝2BE.过B作BF∥CD交AE的延长线为F.当BF＝1时，AB的长为（）

A、4 B、5 C、6 D、7

查看试题解析
9. 如图，△ABE和△CDE是以点E为位似中心的位似图形，已知点A（2，2）、B（3，1）、D（5，2），则点A的对应点C的坐标是（）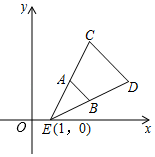

A、（2，3） B、（2，4） C、（3，3） D、（3，4）

查看试题解析
10. 如图，已知抛物线y=ax²+bx+c（a≠0）的对称轴为直线x=﹣1.有下列结论：①b²=4ac ②abc＞0 ③a＞c ④4a+c＞2b.其中结论正确的个数是（）

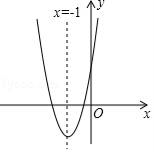A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 化简： $\sqrt{48} - \sqrt{12}$ ＝.

查看试题解析
12. 若一元二次方程x²+bx+5＝0配方后为（x﹣4）²＝k，则k的值为.

查看试题解析
13. 已知点A（4，y₁），B（2，y₂），C（-2，y₃）都在二次函数y=(x-2)²-1的图象上，则y₁ ， y₂ ， y₃的大小关系是.

查看试题解析
14. 已知三个边长分别为1，2，3的正三角形从左到右如图排列，则图中阴影部分面积为．

查看试题解析
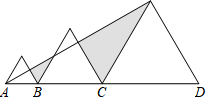15. 如图，在矩形ABCD中，AB＝6，AD＝8，点E是边AD上的一个动点，把△BAE沿BE折叠，点A落在A′处，如果A′恰在矩形的对角线上，则AE的长为.

查看试题解析

三、解答题

16. 计算或解方程

(1)、 $\sqrt{48} \div \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{12} + \sqrt{24}$ ﹣4tan45°；

(2)、x²﹣ $\frac{2}{3}$ x﹣3＝0.

查看试题解析
17. 为弘扬中华传统文化，黔南州近期举办了中小学生“国学经典大赛”．比赛项目为：A．唐诗；B．宋词；C．论语；D．三字经．比赛形式分“单人组”和“双人组”．

(1)、小丽参加“单人组”，她从中随机抽取一个比赛项目，恰好抽中“三字经”的概率是多少？

(2)、小红和小明组成一个小组参加“双人组”比赛，比赛规则是：同一小组的两名队员的比赛项目不能相同，且每人只能随机抽取一次，则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少？请用画树状图或；列表的方法进行说明．

查看试题解析
18. 已知关于x的一元二次方程x²+2（m+1）x+m²﹣2=0．

(1)、若方程有实数根，求实数m的取值范围；

(2)、若m为负整数，求该一元二次方程的解．

查看试题解析
19. 已知抛物线y＝﹣x²﹣2x+3.问：

(1)、该抛物线的顶点坐标是；

(2)、该函数与x轴的交点坐标是，，并在网格中画出该函数的图象；

(3)、x取什么值时，抛物线在x轴上方？

(4)、已知y＝t，t取什么值时与抛物线y＝﹣x²﹣2x+3有两个交点？

查看试题解析
20. 如图①，在我国古建筑的大门上常常悬挂着巨大的匾额，图②中的线段BC就是悬挂在墙壁AM上的某块匾额的截面示意图.已知BC＝1米，∠MBC＝37°.从水平地面点D处看点C，仰角∠ADC＝45°，从点E处看点B，仰角∠AEB＝53°，且DE＝2.4米，求匾额悬挂的高度AB的长.（参考数据：sin37°≈ $\frac{3}{5}$ ，cos37°≈ $\frac{4}{5}$ ，tan37°≈ $\frac{3}{4}$ ）.

查看试题解析
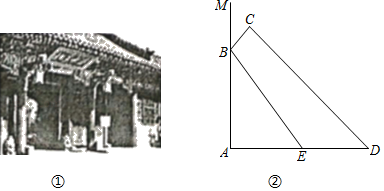21. “互联网+”时代，网上购物备受消费者青睐，某网店专售一款体恤衫，其成本为每件80元，当售价为每件140元时，每月可销售100条，为了吸引更多顾客，该网店采取降价措施，据市场调查反映：销售单价每降1元，则每月可多销售5件，设每件体恤衫的售价为x元（x为正整数），每月的销售量为y件.

(1)、直接写出y与x的函数关系式；

(2)、设该网店每月获得的利润为w元，当销售单价降低多少元时，每月获得的利润最大，最大利润是多少？

(3)、该网店店主热心公益事业，决定每月从利润中捐出400元资助贫困学生，为了保证捐款后每月利润不低于7475元，且让消费者得到最大的实惠，该如何确定体恤衫的销售单价？

查看试题解析
22. 如图①所示，已知正方形ABCD和正方形AEFG，连接DG，BE.

(1)、发现：当正方形AEFG绕点A旋转，如图②所示.
①线段DG与BE之间的数量关系是；

②直线DG与直线BE之间的位置关系是；

(2)、探究：如图③所示，若四边形ABCD与四边形AEFG都为矩形，且AD＝2AB，AG＝2AE时，上述结论是否成立，并说明理由.

(3)、应用：在（2）的情况下，连接BG、DE，若AE＝1，AB＝2，求BG²+DE²的值（直接写出结果）.

查看试题解析
23. 如图：抛物线y＝x²+bx+c与直线y＝﹣x﹣1交于点A，B.其中点B的横坐标为2.点P（m，n）是线段AB上的动点.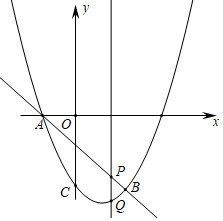

(1)、求抛物线的表达式；

(2)、过点P的直线垂直于x轴，交抛物线于点Q，求线段PQ的长度l与m的关系式，m为何值时，PQ最长？

(3)、在平角直角坐标系中，我们把横、纵坐标都为整数的点称为整点，记顶点都是整点的四边形为整点四边形，在（2）的情况下，在平面内找出所有符合要求的整点R，使P、Q、B、R为整点平行四边形，请直接写出整点R的坐标.

查看试题解析