河南省洛阳市洛宁县2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-03-11 类型：期末考试

进入出卷网下载

一、单选题

1. 已知y=（m+2）x^|m|+2是关于x的二次函数，那么m的值为（）

A、﹣2 B、2 C、±2 D、0

查看试题解析
2. 在二次函数y＝﹣x²+2x+1的图象中，若y随x的增大而减少，则x的取值范围是（）

A、x＜1 B、x＞1 C、x＜﹣1 D、x＞﹣1

查看试题解析
3. 对于二次函数 $y = - \frac{1}{4} x^{2} + x - 4$ ,下列说法正确的是（）

A、当x>0，y随x的增大而增大 B、当x=2时，y有最大值－3 C、图像的顶点坐标为（－2，－7） D、图像与x轴有两个交点

查看试题解析
4. 下列调查方式合适的是（）

A、对空间实验室“天空二号”零部件的检查，采用抽样调查的方式 B、了解炮弹的杀伤力，采用全面调查的方式 C、对中央台“新闻联播”收视率的调查，采用全面调查的方式 D、对石家庄市食品合格情况的调查，采用抽样调查的方式

查看试题解析
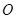5. 如图所示，⊙ 的半径为13，弦AB的长度是24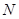， $O N ⊥ A B$ ，垂足为，则ON=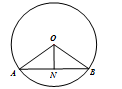

A、5 B、7 C、9 D、11

查看试题解析
6. 如图所示，∠APB＝30°，O为PA上一点，且PO＝6，以点O为圆心，半径为3 $\sqrt{3}$ 的圆与PB的位置关系是（）

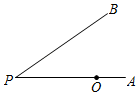A、相离 B、相切 C、相交 D、相切、相离或相交

查看试题解析
7. 如图，线段AB是⊙O的直径，弦CD丄AB，∠CAB=20°，则∠AOD等于（）

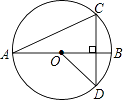A、160° B、150° C、140° D、120°

查看试题解析
8. 如图，AB是半圆的直径，点D是 $\overset{⌢}{A C}$ 的中点，∠ABC＝50°，则∠DAB等于（）

A、65° B、60° C、55° D、50°

查看试题解析
9. 如图，在 Rt△ABC 中BC=2 $\sqrt{2}$ ，以 BC 的中点 O 为圆心的⊙O 分别与 AB，AC 相切于 D，E 两点， $\overset{⌢}{D E}$ 的长为（）

A、 $\frac{π}{4}$ B、 $\frac{π}{2}$ C、π D、2π

查看试题解析
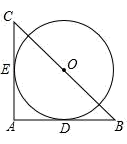10. 如图所示，在直角坐标系中，A点坐标为（-3，-2），⊙A的半径为1，P为x轴上一动点，PQ切⊙A于点Q，则当PQ最小时，P点的坐标为（）

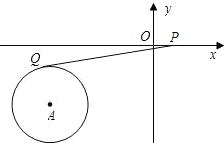A、（-3，0） B、（-2，0） C、（-4，0）或（-2，0） D、（-4，0）

查看试题解析

二、填空题

11. 抛物线y=5（x﹣4）²+3的顶点坐标是．

查看试题解析
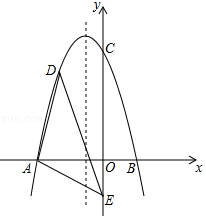
12. 已知二次函数 $y = m x^{2} + x + m (m - 2)$ 的图象经过原点，则 $m$ 的值为.

查看试题解析
13. 二次函数y＝﹣x²+bx+c的部分图象如图所示，由图象可知，不等式﹣x²+bx+c＜0的解集为.

查看试题解析
14. 如图，已知圆周角∠ACB=130°，则圆心角∠AOB= ．

查看试题解析
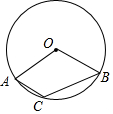15. 如图，在扇形AOB中，∠AOB=90°，点C为OA的中点，CE⊥OA交 $\overset{⌢}{A B}$ 于点E，以点O为圆心，OC的长为半径作 $\overset{⌢}{C D}$ 交OB于点D．若OA=2，则阴影部分的面积为．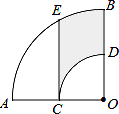

查看试题解析

三、解答题

16. 如图，已知二次函数的顶点为（2， $- 1$ ），且图象经过A（0，3），图象与x轴交于B、C两点.

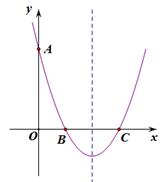(1)、求该函数的解析式；

(2)、连结AB、AC，求△ABC面积.

查看试题解析
17. 已知一个二次函数的图象经过点 $A (- 1, 0)$ 、 $B (3, 0)$ 和 $C (0, - 3)$ 三点.

(1)、求此二次函数的解析式；

(2)、求此二次函数的图象的对称轴和顶点坐标.

查看试题解析
18. “校园安全”受到全社会的广泛关注，某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图，请根据统计图中所提供的信息解答下列问题：

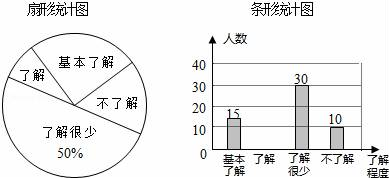(1)、接受问卷调查的学生共有人，扇形统计图中“基本了解”部分所对应扇形的圆心角为度；

(2)、请补全条形统计图；

(3)、若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.

查看试题解析
19. 如图，△ABC是⊙O的内接三角形，BC=4，∠A=30°，求⊙O的直径.

查看试题解析
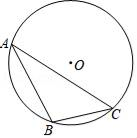20. 某商场购进一种每件价格为90元的新商品，在商场试销时发现：销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系.

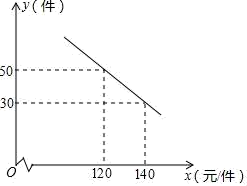(1)、求出y与x之间的函数关系式；

(2)、写出每天的利润W与销售单价x之间的函数关系式，并求出售价定为多少时，每天获得的利润最大？最大利润是多少？

查看试题解析
21. 如图，圆内接四边形ABDC，AB是⊙O的直径，OD⊥BC于E.

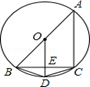(1)、求证：∠BCD=∠CBD；

(2)、若BE=4，AC=6，求DE的长.

查看试题解析
22. 如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC＝BD，连结AC，过点D作DE⊥AC，垂足为E.

(1)、求证：AB＝AC；

(2)、求证：DE为⊙O的切线；

(3)、若⊙O的半径为5，sinB＝ $\frac{4}{5}$ ，求DE的长.

查看试题解析
23. 如图，在平面直角坐标系中，二次函数 $y = a x^{2} + b x + c$ 交 $x$ 轴于点 $A (- 4 ， 0)$ 、 $B (2 ， 0)$ ，交 $y$ 轴于点 $C (0 ， 6)$ ，在 $y$ 轴上有一点 $E (0 ， - 2)$ ，连接 $A E$ .

(1)、求二次函数的表达式；

(2)、若点 $D$ 为抛物线在 $x$ 轴负半轴上方的一个动点，求 $Δ A D E$ 面积的最大值；

(3)、抛物线对称轴上是否存在点 $P$ ，使 $Δ A E P$ 为等腰三角形，若存在，请直接写出所有 $P$ 点的坐标，若不存在请说明理由.

查看试题解析