江苏省盐城市东台市第五联盟2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-03-11 类型:期末考试
一、单选题
-
1. 下面图形表示绿色食品、节水、节能和低碳四个标志,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 点M(﹣5,2)关于x轴对称的坐标是( )A、(﹣5,﹣2) B、(5,﹣2) C、(5,2) D、(﹣5,2)3. 在实数1.732, , , , 中,无理数有( )A、1个 B、2个 C、3个 D、4个4. 点P到△ABC的三个顶点的距离相等,则点P是△ABC ( )的交点.A、三条高 B、三条角平分线 C、三条中线 D、三边的垂直平分线5. 下列说法正确的是( )A、4的平方根是±2 B、8的立方根是±2 C、 D、6. 已知一次函数y=kx+b,函数值y随自变置x的增大而减小,且kb<0,则函数y=kx+b的图象大致是( )
2. 点M(﹣5,2)关于x轴对称的坐标是( )A、(﹣5,﹣2) B、(5,﹣2) C、(5,2) D、(﹣5,2)3. 在实数1.732, , , , 中,无理数有( )A、1个 B、2个 C、3个 D、4个4. 点P到△ABC的三个顶点的距离相等,则点P是△ABC ( )的交点.A、三条高 B、三条角平分线 C、三条中线 D、三边的垂直平分线5. 下列说法正确的是( )A、4的平方根是±2 B、8的立方根是±2 C、 D、6. 已知一次函数y=kx+b,函数值y随自变置x的增大而减小,且kb<0,则函数y=kx+b的图象大致是( )
A、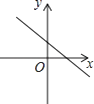 B、
B、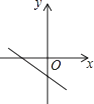 C、
C、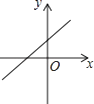 D、
D、 7. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( )
7. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( ) A、9 B、6 C、4 D、38. 如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为( )
A、9 B、6 C、4 D、38. 如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为( ) A、15 B、12.5 C、14.5 D、17
A、15 B、12.5 C、14.5 D、17二、填空题
-
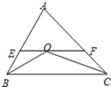
9. 的相反数是 .10. 全球七大洲的总面积约为149 480 000km2 , 对这个数据精确到百万位可表示为km2.11. 若点 若在直线 上,则代数式 的值是.12. 如图,△ABC中,∠B、∠C的平分线交于点O,过O点作EF∥BC交AB、AC于E、F,EF=5,BE=2,则CF=.
 13. 如图, OP平分 , 于点A,点Q是射线OM上一个动点,若PA=3,则PQ的最小值为 .
13. 如图, OP平分 , 于点A,点Q是射线OM上一个动点,若PA=3,则PQ的最小值为 .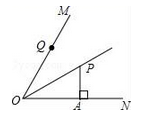 14. 如图,函数 和 的图象相交于点A(m,6),则关于 的不等式 的解集为.
14. 如图,函数 和 的图象相交于点A(m,6),则关于 的不等式 的解集为.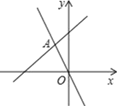 15. 在△ABC中,AB= ,AC=5,若BC边上的高等于3,则BC边的长为 .16. 如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,若AC=3,CE=4,则AD2+BE2=.
15. 在△ABC中,AB= ,AC=5,若BC边上的高等于3,则BC边的长为 .16. 如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,若AC=3,CE=4,则AD2+BE2=.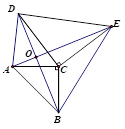 17. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=5,分别以点A、B为圆心,大于 AB的长为半径画弧,两弧交点分别为点P、Q,过P、Q两点作直线交BC于点D,则CD的长是.
17. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=5,分别以点A、B为圆心,大于 AB的长为半径画弧,两弧交点分别为点P、Q,过P、Q两点作直线交BC于点D,则CD的长是.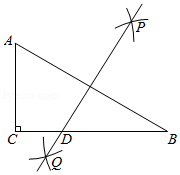 18. 如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,则这块地的面积为 m2.
18. 如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,则这块地的面积为 m2.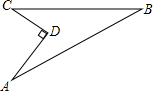
三、解答题
-
19. 计算:20. 解方程:(1)、(x-5)2=64;(2)、(x+1)3-27=021. 如图,在长度为1个单位长度的小正方形组成的正方形网格中,点 、 、 在小正方形的顶点上.
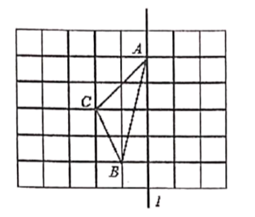
①在图中画出与 关于直线 成轴对称的 ;
②在直线 上找一点 (在答题纸上图中标出),使 的长最短.
22. 如图,在△ABC中, AB的垂直平分线EF交BC于点E,交AB于点F, D为线段CE的中点, BE=AC.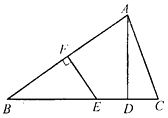 (1)、求证:(2)、若 ,求∠B的度数.
(1)、求证:(2)、若 ,求∠B的度数.
23. 如图,等边三角形 的边长为8,点 是边 上一动点(不与点 重合),以 为边在 的下方作等边三角形 ,连接 .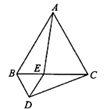 (1)、在运动的过程中, 与 有何数量关系?请说明理由.(2)、当BE=4时,求 的度数.24. 如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)、在运动的过程中, 与 有何数量关系?请说明理由.(2)、当BE=4时,求 的度数.24. 如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.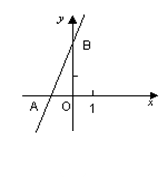 (1)、求△AOB的面积;
(1)、求△AOB的面积;
(2)、过B点作直线BP与x轴相交于P,△ABP的面积是 ,求点P的坐标.
25. 在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1 、y2 (km), y1 、y2 与x的函数关系如图所示.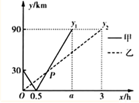 (1)、填空:A、C两港口间的距离为km, ;(2)、求图中点P的坐标;(3)、若两船的距离不超过8km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围.26. 如图
(1)、填空:A、C两港口间的距离为km, ;(2)、求图中点P的坐标;(3)、若两船的距离不超过8km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围.26. 如图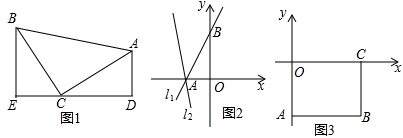 (1)、【模型建立】如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
(1)、【模型建立】如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.求证:△BEC≌△CDA;
(2)、【模型应用】① 已知直线l1:y= x+8与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45 至直线l2 , 如图2,求直线l2的函数表达式;② 如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,-6),点A、C分别在坐标轴上,点P是线段BC上的动点,点D是直线y=-3x+6上的动点且在y轴的右侧.若△APD是以点D为直角顶点的等腰直角三角形,请直接写出点D的坐标.