江苏省盐城市东台市第二联盟2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-03-11 类型:期末考试
一、单选题
-
1. 下列四个图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 点 在y轴上,则点M的坐标为( )A、 B、 C、 D、3. 下列各数中,大小在﹣1和﹣2之间的数是( )A、﹣3 B、﹣ C、0 D、|﹣3|4. 如图,已知AE=CF,BE=DF,要证△ABE≌△CDF,还需添加的一个条件是( )
2. 点 在y轴上,则点M的坐标为( )A、 B、 C、 D、3. 下列各数中,大小在﹣1和﹣2之间的数是( )A、﹣3 B、﹣ C、0 D、|﹣3|4. 如图,已知AE=CF,BE=DF,要证△ABE≌△CDF,还需添加的一个条件是( ) A、∠BAC=∠ACD B、∠ABE=∠CDF C、∠DAC=∠BCA D、∠AEB=∠CFD5. 下列各组数中不能作为直角三角形的三边长的是( )A、1,5, 2, 3 B、7,24,25 C、6,8,10 D、9,12,156. 若直线y=kx+b经过第一、二、四象限,则直线y=bx+k的图象大致是( )A、
A、∠BAC=∠ACD B、∠ABE=∠CDF C、∠DAC=∠BCA D、∠AEB=∠CFD5. 下列各组数中不能作为直角三角形的三边长的是( )A、1,5, 2, 3 B、7,24,25 C、6,8,10 D、9,12,156. 若直线y=kx+b经过第一、二、四象限,则直线y=bx+k的图象大致是( )A、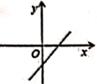 B、
B、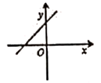 C、
C、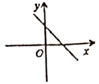 D、
D、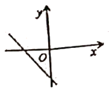 7. 已知一个等腰三角形一内角的度数为 ,则这个等腰三角形顶角的度数为( )A、 B、 C、 或 D、 或8. 如图,在 中, , ,点 在边 上,且 ,点 为 的中点,点 为边 上的动点,当点 在 上移动时,使四边形 周长最小的点 的坐标为( )
7. 已知一个等腰三角形一内角的度数为 ,则这个等腰三角形顶角的度数为( )A、 B、 C、 或 D、 或8. 如图,在 中, , ,点 在边 上,且 ,点 为 的中点,点 为边 上的动点,当点 在 上移动时,使四边形 周长最小的点 的坐标为( )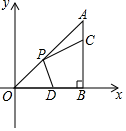 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 的立方根是 .10. 将23 700精确到千位并用科学记数法表示为11. 长方形的一条对角线的长为10cm,一边长为6cm,它的面积是cm2.12. 下列实数:12,- ,|﹣1|, ,0.1010010001…, , 中,有理数有个.13. 把直线 向下平移1个单位,平移后直线的关系式为.14. 一个汽车牌照号码在水中的倒影为
 ,则该车牌照号码为 .
,则该车牌照号码为 .
15. 无论a取什么实数,点A(2a ,6a+1)都在直线l上,则直线l的表达式是.16.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③关于x的方程kx﹣x=a﹣b的解是x=3;④当x<3时,y1<y2中.则正确的序号有 .

三、解答题
-
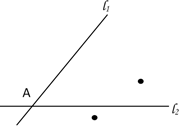
17. 计算:18.(1)、解方程: 3x2-12=0(2)、在实数范围内分解因式:19. 如图,l1、l2交于A点,P、Q的位置如图所示,试确定M点,使它到l1、l2的距离相等,且到P、Q两点的距离也相等.(用直尺和圆规)
 20. 如图,AD为△ABC的中线,AB=AC,∠BAC=45º.过点C 作CE⊥AB,垂足为E,CE与AD交于点F.
20. 如图,AD为△ABC的中线,AB=AC,∠BAC=45º.过点C 作CE⊥AB,垂足为E,CE与AD交于点F. (1)、求证: △AEF≌△CEB;(2)、试探索AF与CD的数量关系,并说明理由.21. 如图,正方形网格的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上.
(1)、求证: △AEF≌△CEB;(2)、试探索AF与CD的数量关系,并说明理由.21. 如图,正方形网格的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上. (1)、分别求出AB,BC,AC的长;(2)、试判断△ABC是什么三角形,并说明理由.22. 已知3x+1的算术平方根是4,x+2y的立方根是-1,
(1)、分别求出AB,BC,AC的长;(2)、试判断△ABC是什么三角形,并说明理由.22. 已知3x+1的算术平方根是4,x+2y的立方根是-1,
(1)、求x、y的值;(2)、求2x-5y的平方根.
23. 某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用8000元购进电冰箱的数量与用6400元购进空调的数量相等.(1)、求每台电冰箱与空调的进价分别是多少?(2)、已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,其中购进电冰箱x台(33≤x≤40),那么该商店要获得最大利润应如何进货?24. 如图,AB=AC,∠A=120º,BC=6cm,ED、FG分别是AB,AC的垂直平分线,求BE的长. 25. 如图,已知直线y=﹣2x+8与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.
25. 如图,已知直线y=﹣2x+8与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.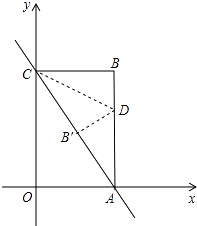 (1)、求点A、C的坐标;(2)、将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式;
(1)、求点A、C的坐标;(2)、将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式;
(3)、在(2)的条件下,坐标平面内是否存在点P(除点B外),使得△APC与△ABC全等?若存在,直接写出符合条件的点P的坐标;若不存在,请说明理由.26. 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒. (1)、出发2秒后,求△ABP的周长.(2)、问t为何值时,△BCP为等腰三角形?(3)、另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
(1)、出发2秒后,求△ABP的周长.(2)、问t为何值时,△BCP为等腰三角形?(3)、另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?