江苏省盐城市大丰区2019-2020学年八年级上学期期末数学试卷
试卷更新日期:2020-03-11 类型:期末考试
一、单选题
-
1. 在以下永洁环保、绿色食品、节能、绿色环保四个标志中,是轴对称图形是( )A、
 B、
B、 C、
C、 D、
D、 2. 7的平方根是( )A、 ±7 B、7 C、-7 D、±3. 下列各点中在第四象限的是( )A、 B、 C、 D、4. 如图,∠A=30°,∠C′=60°,△ABC 与△A′B′C′关于直线l对称,则∠B度数为( )
2. 7的平方根是( )A、 ±7 B、7 C、-7 D、±3. 下列各点中在第四象限的是( )A、 B、 C、 D、4. 如图,∠A=30°,∠C′=60°,△ABC 与△A′B′C′关于直线l对称,则∠B度数为( )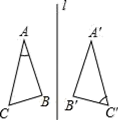 A、 B、 C、 D、5. 如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
A、 B、 C、 D、5. 如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
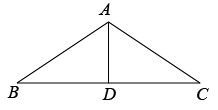 A、5 B、6 C、8 D、106.
A、5 B、6 C、8 D、106.如图,在△ABC中,AB=AC,AB+BC=8.将△ABC折叠,使得点A落在点B处,折痕DF分别与AB、AC交于点D、F,连接BF,则△BCF的周长是( )
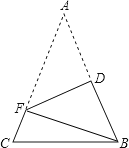 A、8 B、16 C、4 D、107. 某种鲸的体重约为 ,关于这个近似数,下列说法正确的是( )A、精确到百分位 B、精确到0.01 C、精确到千分位 D、精确到千位8. 如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组 的解为( )
A、8 B、16 C、4 D、107. 某种鲸的体重约为 ,关于这个近似数,下列说法正确的是( )A、精确到百分位 B、精确到0.01 C、精确到千分位 D、精确到千位8. 如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组 的解为( )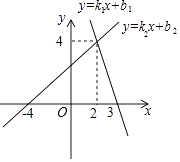 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如果 有意义,那么x可以取的最小整数为.10. 矩形ABCD中,其中三个顶点的坐标分别是(0,0)、(5,0)、(5,3),则第四个顶点的坐标是.11. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为2,5,1,2.则最大的正方形E的面积是.
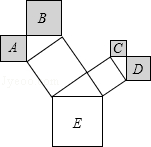 12. 在平面直角坐标系中,点A(2,1)向左平移3个单位长度,再向下平移4个单位后的坐标为.13. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了步路(假设2步为1米),却踩伤了花草.
12. 在平面直角坐标系中,点A(2,1)向左平移3个单位长度,再向下平移4个单位后的坐标为.13. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了步路(假设2步为1米),却踩伤了花草. 14. 如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为 .
14. 如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为 .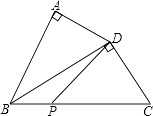 15. 如图,OA、BA分别表示甲、乙两名学生运动的一次函数图象,图中s(m)和t(s)分别表示运动路程和时间,根据图象,判断快者的速度比慢者的速度每秒快.
15. 如图,OA、BA分别表示甲、乙两名学生运动的一次函数图象,图中s(m)和t(s)分别表示运动路程和时间,根据图象,判断快者的速度比慢者的速度每秒快.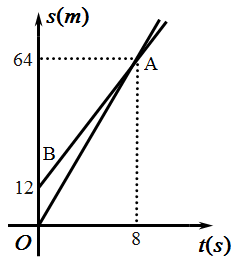 16. 在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点,已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m,当m=3时,则点B的横坐标是 .
16. 在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点,已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m,当m=3时,则点B的横坐标是 .
三、解答题
-
17. 计算:(1)、(2)、(3)、18. 如图,在 中, ,垂足为点 , , , .
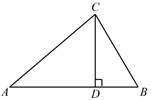 (1)、求 的长;(2)、求 的长.19. 已知:如图,AB⊥BC,DC⊥BC,B、C分别是垂足,DE交AC于M,BC=CD,AB=EC,DE与AC有什么关系?请说明理由.
(1)、求 的长;(2)、求 的长.19. 已知:如图,AB⊥BC,DC⊥BC,B、C分别是垂足,DE交AC于M,BC=CD,AB=EC,DE与AC有什么关系?请说明理由.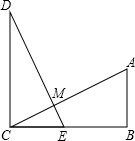 20. 规定:在平面直角坐标系中,将一个图形先关于y轴对称,再向下平移2个单位记为1次“R变换”.如图,已知△ABC的三个顶点均在格点上,其中点B的坐标为(1,2).
20. 规定:在平面直角坐标系中,将一个图形先关于y轴对称,再向下平移2个单位记为1次“R变换”.如图,已知△ABC的三个顶点均在格点上,其中点B的坐标为(1,2).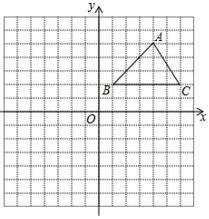 (1)、画出△ABC经过1次“R变换”后的图形△A1B1C1;(2)、若△ABC经过3次“R变换”后的图形为△A3B3C3 , 则顶点A3坐标为.21. 如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)、画出△ABC经过1次“R变换”后的图形△A1B1C1;(2)、若△ABC经过3次“R变换”后的图形为△A3B3C3 , 则顶点A3坐标为.21. 如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.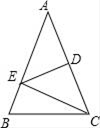 (1)、求∠ECD的度数;(2)、若CE=5,求BC的长.22. 如图,一次函数y=(m+1)x+ 的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB的面积为 .
(1)、求∠ECD的度数;(2)、若CE=5,求BC的长.22. 如图,一次函数y=(m+1)x+ 的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB的面积为 .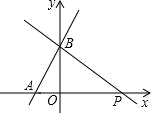 (1)、求m的值及点A的坐标;(2)、过点B作直线BP与x轴的正半轴相交于点P,且OP=3OA,求直线BP的解析式.23. 如图是一块地的平面图,AD=4m,CD=3m,AB=13m,BC=12m,∠ADC=90°,求这块地的面积.
(1)、求m的值及点A的坐标;(2)、过点B作直线BP与x轴的正半轴相交于点P,且OP=3OA,求直线BP的解析式.23. 如图是一块地的平面图,AD=4m,CD=3m,AB=13m,BC=12m,∠ADC=90°,求这块地的面积.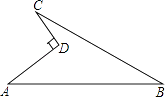 24. 如图,△ABC中,∠A=90°,D为AC上一点,E为BC上一点,点A和点E关于BD对称,点B和点C关于DE对称.求∠ABC和∠C的度数.
24. 如图,△ABC中,∠A=90°,D为AC上一点,E为BC上一点,点A和点E关于BD对称,点B和点C关于DE对称.求∠ABC和∠C的度数.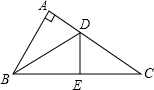 25. 已知函数y1=2x-4与y2=-2x+8的图象,观察图象并回答问题:
25. 已知函数y1=2x-4与y2=-2x+8的图象,观察图象并回答问题: (1)、x取何值时,2x-4>0?(2)、x取何值时,-2x+8>0?(3)、x取何值时,2x-4>0与-2x+8>0同时成立?(4)、求函数y1=2x-4与y2=-2x+8的图象与x轴所围成的三角形的面积?26. 如图所示是甲乙两个工程队完成某项工程的进度图,首先是甲独做了10天,然后两队合做,完成剩下的工程.
(1)、x取何值时,2x-4>0?(2)、x取何值时,-2x+8>0?(3)、x取何值时,2x-4>0与-2x+8>0同时成立?(4)、求函数y1=2x-4与y2=-2x+8的图象与x轴所围成的三角形的面积?26. 如图所示是甲乙两个工程队完成某项工程的进度图,首先是甲独做了10天,然后两队合做,完成剩下的工程.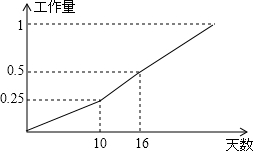 (1)、甲队单独完成这项工程,需要多少天?(2)、求乙队单独完成这项工程需要的天数;(3)、实际完成的时间比甲独做所需的时间提前多少天?27. 建立模型:如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.
(1)、甲队单独完成这项工程,需要多少天?(2)、求乙队单独完成这项工程需要的天数;(3)、实际完成的时间比甲独做所需的时间提前多少天?27. 建立模型:如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.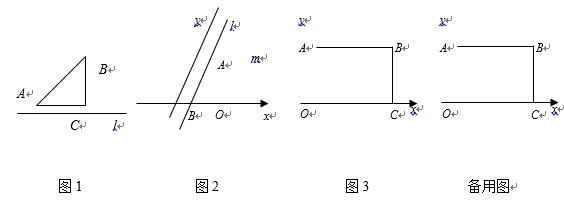 (1)、操作:
(1)、操作:过点A作AD⊥ 于点D,过点B作BE⊥ 于点E.求证:△CAD≌△BCE.
(2)、模型应用:①如图2,在直角坐标系中,直线 : 与y轴交于点A,与x轴交于点B,将直线 绕着点A顺时针旋转45°得到直线 .求直线 的函数表达式.
②如图3,在直角坐标系中,点B(4,3),作BA⊥y轴于点A,作BC⊥x轴于点C,P是直线BC上的一个动点,点Q(a,5a﹣2)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.