江苏省连云港市赣榆区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-03-11 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点 关于 轴的对称点的坐标是( )A、 B、 C、 D、2. 下列四组线段中,可以构成直角三角形的是( )A、4,5,6 B、2,3,4 C、 ,3,4 D、1, ,33. 下列无理数中,在﹣1与2之间的是( )A、﹣ B、﹣ C、 D、4. 下列运算正确的是( )A、 =2 B、|﹣3|=﹣3 C、 =±2 D、 =35. 一次函数y=-5x+3的图象经过的象限是( )A、一、二、三 B、二、三、四 C、一、二、四 D、一、三、四6. 如图,矩形ABCD中,AB=6,BC=12,如果将该矩形沿对角线BD折叠,那么图中阴影部分△BED的面积是( )
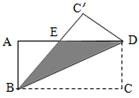 A、18 B、22.5 C、36 D、457. 如图, 为 边 上一点, , ,且 , ,则 等于( )
A、18 B、22.5 C、36 D、457. 如图, 为 边 上一点, , ,且 , ,则 等于( ) A、 B、 C、 D、8. 在一次800米的长跑比赛中,甲、乙两人所跑的路程 (米)与各自所用时间 (秒)之间的函数图象分别为线段 和折线 ,则下列说法不正确的是( )
A、 B、 C、 D、8. 在一次800米的长跑比赛中,甲、乙两人所跑的路程 (米)与各自所用时间 (秒)之间的函数图象分别为线段 和折线 ,则下列说法不正确的是( ) A、甲的速度保持不变 B、乙的平均速度比甲的平均速度大 C、在起跑后第180秒时,两人不相遇 D、在起跑后第50秒时,乙在甲的前面
A、甲的速度保持不变 B、乙的平均速度比甲的平均速度大 C、在起跑后第180秒时,两人不相遇 D、在起跑后第50秒时,乙在甲的前面二、填空题
-
9. 如果点P(m+1,m+3)在y轴上,则m= .10. 等腰三角形的一个外角是80°,则其底角是度.11. 在 , , ,0,0.454454445…, 中,无理数有个.12. 圆周率π=3.1415926…精确到千分位的近似数是.13. 已知实数 、 满足 ,则代数式 的值为.14. 将函数y=3x+1的图象沿y轴向下平移2个单位长度,所得直线的函数表达式为 .
15. 在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组 的解是. 16. 如图,在平面直角坐标系中,点P(﹣1,a)在直线y=2x+2与直线y=2x+4之间,则a的取值范围是.
16. 如图,在平面直角坐标系中,点P(﹣1,a)在直线y=2x+2与直线y=2x+4之间,则a的取值范围是.
三、解答题
-
17. 计算: .18. 求下列各式中的 :(1)、 ;(2)、 .19. 已知 与 成正比,且当 时, .(1)、求 与 之间的函数关系式;(2)、若点 在这个函数图象上,求 的值.20. 如图,点 在线段 上, , , . 平分 .
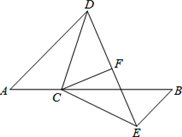
求证:
(1)、 ;(2)、 .21. 某学校要对如图所示的一块地进行绿化,已知 , , , , ,求这块地的面积.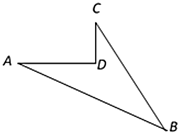 22. 如图,一次函数 与正比例函数 的图像交于点 .
22. 如图,一次函数 与正比例函数 的图像交于点 . (1)、求正比例函数和一次函数的解析式;(2)、根据图像,写出关于 的不等式 的解集;(3)、求 的面积.23. 某学校是乒乓球体育传统项目校,为进一步推动该项目的发展.学校准备到体育用品店购买甲、乙两种型号乒乓球若干个,已知3个甲种乒乓球和5个乙种乒乓球共需50元,2个甲种乒乓球和3个乙种乒乓球共需31元.(1)、求1个甲种乒乓球和1个乙种乒乓球的售价各是多少元?(2)、学校准备购买这两种型号的乒乓球共200个,要求甲种乒乓球的数量不超过乙种乒乓球的数量的3倍,请设计出最省钱的购买方案,并说明理由.24. 已知:如图,点 在 的边 上,且 .
(1)、求正比例函数和一次函数的解析式;(2)、根据图像,写出关于 的不等式 的解集;(3)、求 的面积.23. 某学校是乒乓球体育传统项目校,为进一步推动该项目的发展.学校准备到体育用品店购买甲、乙两种型号乒乓球若干个,已知3个甲种乒乓球和5个乙种乒乓球共需50元,2个甲种乒乓球和3个乙种乒乓球共需31元.(1)、求1个甲种乒乓球和1个乙种乒乓球的售价各是多少元?(2)、学校准备购买这两种型号的乒乓球共200个,要求甲种乒乓球的数量不超过乙种乒乓球的数量的3倍,请设计出最省钱的购买方案,并说明理由.24. 已知:如图,点 在 的边 上,且 . (1)、求证: ;(2)、若 的平分线 交 于点 , 交 于点 ,设 , ,求 的长.25. 甲、乙两地间的直线公路长为 千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发 小时,途中轿车出现了故障,停下维修,货车仍继续行驶. 小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离 (千米)与轿车所用的时间 (小时)的关系如图所示,请结合图象解答下列问题:
(1)、求证: ;(2)、若 的平分线 交 于点 , 交 于点 ,设 , ,求 的长.25. 甲、乙两地间的直线公路长为 千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发 小时,途中轿车出现了故障,停下维修,货车仍继续行驶. 小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离 (千米)与轿车所用的时间 (小时)的关系如图所示,请结合图象解答下列问题: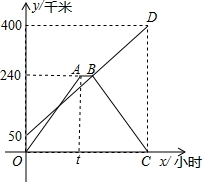 (1)、货车的速度是千米/小时;轿车的速度是千米/小时; 值为.(2)、求轿车距其出发地的距离 (千米)与所用时间 (小时)之间的函数关系式并写出自变量 的取值范围;(3)、请直接写出货车出发多长时间两车相距 千米.26.(1)、【模型建立】
(1)、货车的速度是千米/小时;轿车的速度是千米/小时; 值为.(2)、求轿车距其出发地的距离 (千米)与所用时间 (小时)之间的函数关系式并写出自变量 的取值范围;(3)、请直接写出货车出发多长时间两车相距 千米.26.(1)、【模型建立】如图1,等腰直角三角形 中, , ,直线 经过点 ,过 作 于点 ,过 作 于点 .

求证: ;
(2)、【模型应用】①已知直线 : 与 轴交于点 ,与 轴交于点 ,将直线 绕着点 逆时针旋转 至直线 ,如图2,求直线 的函数表达式;

②如图3,在平面直角坐标系中,点 ,作 轴于点 ,作 轴于点 , 是线段 上的一个动点,点 是直线 上的动点且在第一象限内.问点 、 、 能否构成以点 为直角顶点的等腰直角三角形,若能,请直接写出此时点 的坐标,若不能,请说明理由.
