湖北省孝感市安陆市2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-03-11 类型:期末考试
一、单选题
-
1. 计算 的结果是( )A、 B、 C、 D、2. 若分式 有意义,则 的取值范围是( )A、 B、 C、 D、3. 若 ,则 的值为( )A、3 B、6 C、9 D、124. 点P(m,-2)与点P1(-4,n)关于x轴对称,则m,n的值分别为( )A、 , B、 , C、 , D、 ,5. 如果 ,那么代数式 的值为( )A、-3 B、-1 C、1 D、36. 已知图中的两个三角形全等,则∠1等于( )
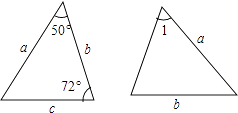 A、72° B、60° C、50° D、58°7. 如图,在小正三角形组成的网格中,已有 个小正三角形涂黑,还需涂黑 个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰有三条对称轴,则 的最小值为( )
A、72° B、60° C、50° D、58°7. 如图,在小正三角形组成的网格中,已有 个小正三角形涂黑,还需涂黑 个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰有三条对称轴,则 的最小值为( )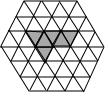 A、 B、 C、 D、8. 如图所示,在等边△ABC中,D,E分别是BC,AC的中点,点P是线段AD上的一个动点,当△PCE的周长最小时,P点的位置在( )
A、 B、 C、 D、8. 如图所示,在等边△ABC中,D,E分别是BC,AC的中点,点P是线段AD上的一个动点,当△PCE的周长最小时,P点的位置在( )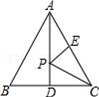 A、△ABC的重心处 B、AD的中点处 C、A点处 D、D点处9. 已知三个实数a,b,c满足a-2b+c=0,a+2b+c<0,则( )A、b>0,b2-ac≤0 B、b<0,b2-ac≤0 C、b>0,b2-ac≥0 D、b<0,b2-ac≥010. 如图,已知△ABC中,AB=7,AC=5,BC=3,在△ABC所在平面内一条直线,将△ABC分割成两个三角形,使其中有一个边长为3的等腰三角形,则这样的直线最多可画( )
A、△ABC的重心处 B、AD的中点处 C、A点处 D、D点处9. 已知三个实数a,b,c满足a-2b+c=0,a+2b+c<0,则( )A、b>0,b2-ac≤0 B、b<0,b2-ac≤0 C、b>0,b2-ac≥0 D、b<0,b2-ac≥010. 如图,已知△ABC中,AB=7,AC=5,BC=3,在△ABC所在平面内一条直线,将△ABC分割成两个三角形,使其中有一个边长为3的等腰三角形,则这样的直线最多可画( )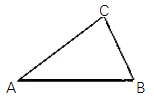 A、2条 B、3条 C、4条 D、5条
A、2条 B、3条 C、4条 D、5条二、填空题
-
11. 因式分解:a3+2a2+a= .12. 人体中红细胞的直径约为0.0000077 m,数据0.0000077用科学记数法表示为13. 如图,在 中, 是边 上的高, 平分 ,交 于点 , , ,则 的面积为.
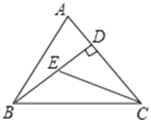 14. 如图,在 中, , , 的平分线 交 于点 , ,交 的延长线于点 ,若 ,则 .15. 如图所示的网格是正方形网格,则 =°(点A,B,P是网格线交点).
14. 如图,在 中, , , 的平分线 交 于点 , ,交 的延长线于点 ,若 ,则 .15. 如图所示的网格是正方形网格,则 =°(点A,B,P是网格线交点).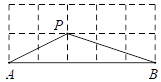 16. 如图,第n个图形是由正n+2边形“扩展”而来(n=1,2,3,4…),第n个图形中共有个顶点(结果用含n的式子表示).
16. 如图,第n个图形是由正n+2边形“扩展”而来(n=1,2,3,4…),第n个图形中共有个顶点(结果用含n的式子表示).
三、解答题
-
17. 先化简,再求值: ,其中 .18. 解方程:
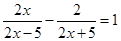 . 19. 观察以下等式:
. 19. 观察以下等式:第1个等式: ,
第2个等式: ,
第3个等式: ,
第4个等式: ,
第5个等式: ,
……按照以上规律,解决下列问题:
(1)、写出第6个等式:;(2)、写出你猜想的第n个等式(用含n的等式表示),并证明.20. 如图, 中, , ,一同学利用直尺和圆规完成如下操作:分别以点 、 为圆心,以大于 的长为半径画弧,两弧交于点 , 两点,直线 交 于 ,交 于 .请你观察图形,猜想 与 之间的数量关系,并证明你的结论.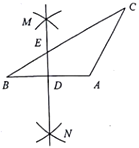 21. 从安陆到武汉市,可乘坐普通列车或高铁,已知高铁的行驶路程是100千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.(1)、求普通列车的行驶路程;(2)、设计高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短45分钟,求高铁的平均速度.22.(1)、计算:(2)、已知: , ,
21. 从安陆到武汉市,可乘坐普通列车或高铁,已知高铁的行驶路程是100千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.(1)、求普通列车的行驶路程;(2)、设计高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短45分钟,求高铁的平均速度.22.(1)、计算:(2)、已知: , ,①求 的值;
②求 的值.
23. 仔细阅读下面的例题,并解答问题:例题:已知二次三项式 有一个因式是 ,求另一个因式以及 的值.
解法一:设另一个因式为 ,得
则 ,
∴ 解得 , .
∴另一个因式为 , 的值为-21.
解法二:设另一个因式为 ,得
∴当 时,
即 ,解得
∴
∴另一个因式为 , 的值为-21.
问题:仿照以上一种方法解答下面问题.
(1)、若多项式 分解因式的结果中有因式 ,则实数 .(2)、已知二次三项式 有一个因式是 ,求另一个因式及 的值.24. 如图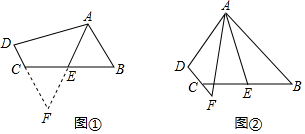 (1)、如图①,在四边形 中, ,点 是 的中点,若 是 的平分线,试判断 , , 之间的等量关系.
(1)、如图①,在四边形 中, ,点 是 的中点,若 是 的平分线,试判断 , , 之间的等量关系.解决此问题可以用如下方法:延长 交 的延长线于点 ,易证 得到 ,从而把 , , 转化在一个三角形中即可判断. , , 之间的等量关系;
(2)、问题探究:如图②,在四边形 中, , 与 的延长线交于点 ,点 是 的中点,若 是 的平分线,试探究 , , 之间的等量关系,并证明你的结论.