湖北省武汉市江汉区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-03-11 类型:期末考试
一、单选题
-
1. 下列图形是公共设施标志,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 用科学记数法表示数0.000 012,正确的是( )A、 B、 C、 D、3. 如图,把一张长方形的纸沿对角线BD折叠,使点C落到点 的位置,若 平分 ,则 的度数是( )
2. 用科学记数法表示数0.000 012,正确的是( )A、 B、 C、 D、3. 如图,把一张长方形的纸沿对角线BD折叠,使点C落到点 的位置,若 平分 ,则 的度数是( )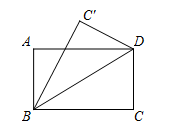 A、15° B、30° C、45° D、60°4. 下列分式中,x取任意实数都有意义的是( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 如图, , ,则下列结论不一定成立的是( )
A、15° B、30° C、45° D、60°4. 下列分式中,x取任意实数都有意义的是( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 如图, , ,则下列结论不一定成立的是( ) A、 ⊥ B、 C、 D、7. 已知甲做360个零件与乙做480个零件所用的时间相同,两人每天共做140个零件,设甲每天做x个零件,根据题意,可列方程为( )A、 B、 C、 D、8. 如图,在△ABC中,进行如下操作:①分别以点A和点C为圆心,以大于 的长为半径作弧,两弧分别相交于点M,N;②作直线MN,交线段AC于点D;③连接BD.则下列结论正确的是( )
A、 ⊥ B、 C、 D、7. 已知甲做360个零件与乙做480个零件所用的时间相同,两人每天共做140个零件,设甲每天做x个零件,根据题意,可列方程为( )A、 B、 C、 D、8. 如图,在△ABC中,进行如下操作:①分别以点A和点C为圆心,以大于 的长为半径作弧,两弧分别相交于点M,N;②作直线MN,交线段AC于点D;③连接BD.则下列结论正确的是( ) A、BD平分∠ABC B、BD⊥AC C、AD=CD D、△ABD≌△CBD9. 下列分式中,把x、y的值同时扩大2倍后,结果也扩大为原来的2倍的是( )A、 B、 C、 D、10. 式子 的值不可能为( )A、 B、0 C、1 D、3
A、BD平分∠ABC B、BD⊥AC C、AD=CD D、△ABD≌△CBD9. 下列分式中,把x、y的值同时扩大2倍后,结果也扩大为原来的2倍的是( )A、 B、 C、 D、10. 式子 的值不可能为( )A、 B、0 C、1 D、3二、填空题
-
11. 分式 和 的最简公分母是.12. 若分式 的值为正数,则 的取值范围为.13. 若等腰三角形的一个角为80°,则它的顶角为.14. 已知△ABC的面积为S,BC的长为a,AD为BC边上的高,则AD的长度用含S,a的式子表示为.15. 如图,在△ABC中,若BC=6,AC=4,AB边的垂直平分线交AB于点E,交BC于点D,则△ADC的周长是.
 16. 如图,点O是△ABC角平分线的交点,过点O作MN∥BC分别与AB,AC相交于点M,N,若 , , ,则△AMN的周长为.
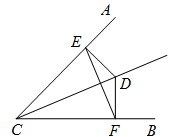
16. 如图,点O是△ABC角平分线的交点,过点O作MN∥BC分别与AB,AC相交于点M,N,若 , , ,则△AMN的周长为. 17. 如图,点D,E,F分别在等边三角形ABC的三边上,且DE⊥AB,EF⊥BC,FD⊥AC,过点F作FH⊥AB于H,则 的值为.
17. 如图,点D,E,F分别在等边三角形ABC的三边上,且DE⊥AB,EF⊥BC,FD⊥AC,过点F作FH⊥AB于H,则 的值为. 18. 关于x的方程 无解,则 .19. 已知分式 化简后的结果是一个整式,则常数 =.20. 如图, ,四边形ABCD的顶点A在 的内部,B,C两点在OM上(C在B,O之间),且 ,点D在ON上,若当CD⊥OM时,四边形ABCD的周长最小,则此时AD的长度是.
18. 关于x的方程 无解,则 .19. 已知分式 化简后的结果是一个整式,则常数 =.20. 如图, ,四边形ABCD的顶点A在 的内部,B,C两点在OM上(C在B,O之间),且 ,点D在ON上,若当CD⊥OM时,四边形ABCD的周长最小,则此时AD的长度是.
三、解答题
-
21. 因式分解:(1)、 ;(2)、 .22. 解下列方程:(1)、 ;(2)、 .23. 如图,D为∠ACB平分线上一点,DE⊥CA于E,DF⊥CB于F.试探究CD与EF的位置关系,并证明你的结论.
 24.(1)、计算: ;(2)、若x为整数,且 ,求(1)中式子的值.25. 如图,在平面直角坐标系中,△ABC的三个顶点为 A(2,2),B(5,3),C(3,5).
24.(1)、计算: ;(2)、若x为整数,且 ,求(1)中式子的值.25. 如图,在平面直角坐标系中,△ABC的三个顶点为 A(2,2),B(5,3),C(3,5). (1)、请作出△ABC关于y轴的对称图形△A1B1C1 , 并写出点A的对称点A1的坐标;(2)、点M是第一象限内一点(不与点A重合),且M点的横、纵坐标都为整数.
(1)、请作出△ABC关于y轴的对称图形△A1B1C1 , 并写出点A的对称点A1的坐标;(2)、点M是第一象限内一点(不与点A重合),且M点的横、纵坐标都为整数.①若 ,请直接写出一个满足条件的M点的坐标;
②若 ,请直接写出一个满足条件的M点的坐标;
(3)、将△A1B1C1向右平移n个单位长度得到△A2B2C2 , 若△ABC与△A2B2C2关于某条直线l对称,则直线l与x轴交点的横坐标为(用含n的式子表示).26. 用电脑程序控制小型赛车进行比赛,“复兴号”和“和谐号”两辆赛车进入了决赛.两辆赛车从距离终点75米的某地同时出发,“复兴号”比“和谐号”早t秒到达终点,且“复兴号”的平均速度是“和谐号”的m倍.(1)、当m=1.2,t=5时,求“复兴号”的平均速度是多少米/秒?(2)、“和谐号”的平均速度为米/秒(用含m、t的式子表示).27. 已知△ABC是等边三角形,点D在BC边上,点E在AB的延长线上,将DE绕D点顺时针旋转120°得到DF. (1)、如图1,若点F恰好落在AC边上,求证:点D是BC的中点;(2)、如图2,在(1)的条件下,若 =45°,连接AD,求证: ;(3)、如图3,若 ,连CF,当CF取最小值时,直接写出 的值.28. 在平面直角坐标系中,已知点 , 与坐标原点O在同一直线上,且AO=BO,其中m,n满足 .
(1)、如图1,若点F恰好落在AC边上,求证:点D是BC的中点;(2)、如图2,在(1)的条件下,若 =45°,连接AD,求证: ;(3)、如图3,若 ,连CF,当CF取最小值时,直接写出 的值.28. 在平面直角坐标系中,已知点 , 与坐标原点O在同一直线上,且AO=BO,其中m,n满足 . (1)、求点A,B的坐标;(2)、如图1,若点M,P分别是x轴正半轴和y轴正半轴上的点,点P的纵坐标不等于2,点N在第一象限内,且 ,PA⊥PN, ,求证:BM⊥MN;(3)、如图2,作AC⊥y轴于点C,AD⊥x轴于点D,在CA延长线上取一点E,使 ,连结BE交AD于点F,恰好有 ,点G是CB上一点,且 ,连结FG,求证: .
(1)、求点A,B的坐标;(2)、如图1,若点M,P分别是x轴正半轴和y轴正半轴上的点,点P的纵坐标不等于2,点N在第一象限内,且 ,PA⊥PN, ,求证:BM⊥MN;(3)、如图2,作AC⊥y轴于点C,AD⊥x轴于点D,在CA延长线上取一点E,使 ,连结BE交AD于点F,恰好有 ,点G是CB上一点,且 ,连结FG,求证: .