湖北省省直辖县级行政单位潜江市潜江市三市联考2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2020-03-11 类型：期末考试

进入出卷网下载

一、单选题

1. 计算x⁶•x²的结果是（）

A、x³ B、x⁴ C、x⁸ D、x¹²

查看试题解析
2. 要使分式 $\frac{2}{x - 1}$ 有意义，则x的取值范围为（）

A、x＞1 B、x≥1 C、x≠1 D、x＝1

查看试题解析
3. 根据图①的面积可以说明多项式的乘法运算（2a+b）（a+b）＝2a²+3ab+b² ，那么根据图②的面积可以说明多项式的乘法运算是（）

A、（a+3b）（a+b）＝a²+4ab+3b² B、（a+3b）（a+b）＝a²+3b² C、（b+3a）（b+a）＝b²+4ab+3a² D、（a+3b）（a﹣b）＝a²+2ab﹣3b²

查看试题解析
4. 已知一个三角形的两边长为5和10，则第三边的长可以为（）

A、5 B、10 C、15 D、20

查看试题解析
5. 下列各式中，正确的是（）

A、 $\frac{b}{a} = \frac{b^{2}}{a^{2}}$ B、 $\frac{a^{2} + b^{2}}{a + b} = a + b$ C、 $\frac{2 y}{2 x + y} = \frac{y}{x + y}$ D、 $\frac{1}{- x + y} = - \frac{1}{x - y}$

查看试题解析
6. 已知一个多边形的内角和是1080°，则这个多边形是（）

A、五边形 B、六边形 C、七边形 D、八边形

查看试题解析
7. 将点A（3，2）沿x轴向左平移4个单位长度得到点A′，点A′关于y轴对称的点的坐标是

A、（﹣3，2） B、（﹣1，2） C、（1，2） D、（1，﹣2）

查看试题解析
8.
如图，∠ABC=50°，BD平分∠ABC，过D作DE∥AB交BC于点E，若点F在AB上，且满足DF=DE，则∠DFB的度数为（　　）

A、25° B、130° C、50°或130° D、25°或130°

查看试题解析
9.
如图是一个台球桌面的示意图，图中四个角上的阴影部分分别表示四个入球孔．若一个球按图中所示的方向被击出（球可以经过多次反射），则该球最后将落入的球袋是（　　）

A、1号袋 B、2号袋 C、3号袋 D、4号袋

查看试题解析
10. 如图，边长为24的等边三角形ABC中，M是高CH所在直线上的一个动点，连结MB，将线段BM绕点B逆时针旋转60°得到BN，连结HN.则在点M运动过程中，线段HN长度的最小值是（）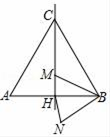

A、12 B、6 C、3 D、1

查看试题解析

二、填空题

11. 在我们的生活中处处有数学的身影，请看图，折叠一张三角形纸片，把三角形的三个角拼在一起，就得到一个著名的几何定理，请你写出这一定理.

查看试题解析
12. 数0.000301用科学记数法表示为.

查看试题解析
13. 因式分解：x³-9x=.

查看试题解析
14. 已知 $a - b = 4$ ， $a b + c^{2} + 4 = 0$ ，则 $a + b + c =$ .

查看试题解析
15. 如图，Rt△ABC纸片中，∠C＝90°，点D在BC上，沿AD折叠，点C恰好落在AB上的点E处，已知BC＝24，∠B＝30°，则DE的长是.

查看试题解析
16. 如图，△ABC的面积为1.第一次操作：分别延长AB，BC，CA至点A₁ ， B₁ ， C₁ ，使A₁B＝AB，B₁C＝BC，C₁A＝CA，顺次连结A₁ ， B₁ ， C₁ ，得到△A₁B₁C₁.第二次操作：分别延长A₁B₁ ， B₁C₁ ， C₁A₁至点A₂ ， B₂ ， C₂ ，使A₂B₁＝A₁B₁ ， B₂C₁＝B₁C₁ ， C₂A₁＝C₁A₁ ，顺次连结A₂ ， B₂ ， C₂ ，得到△A₂B₂C₂.…按此规律，要使得到的三角形的面积超过2013，最少经过次操作.

查看试题解析

三、解答题

17. 解方程： $\frac{1}{x + 1} + \frac{2}{x - 1} = \frac{4}{x^{2} - 1}$

查看试题解析
18. 先化简，再求值：

(1)、（a²b﹣2ab²﹣b³）÷b﹣（a+b）（a﹣b），其中a＝1，b＝﹣2.

(2)、先化简（1+ $\frac{2}{x - 3}$ ）÷ $\frac{x^{2} - 1}{x^{2} - 6 x + 9}$ ，再从﹣1，0，1，2，3中选取一个合适的数作为x的值代入求值.

查看试题解析
19. 如图，在△ABC中，∠B＝2∠C，AE平分∠BAC交BC于点E.

(1)、如图①，若AD⊥BC于点D，∠C＝40°，求∠DAE的度数；

(2)、如图②，若EF⊥AE交AC于点F，求证：∠C＝2∠FEC.

查看试题解析
20. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（﹣4，5），（﹣1，3）.

(1)、①在如图所示的网格平面内作出平面直角坐标系，标注原点以及x轴、y轴；
②作出△ABC关于y轴对称的△A′B′C′，并写出点B′的坐标；

(2)、如图（2）点P是x轴上的动点，在图中找出使△A′BP周长最小时的点P，直接写出点P的坐标是：.

查看试题解析
21. 如图，在△ABC中，∠BAC＝90°，E为边BC上的点，且AB＝AE，D为线段BE的中点，过点E作EF⊥AE，过点A作AF∥BC，且AF、EF相交于点F.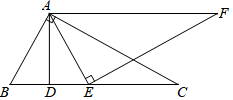

(1)、求证：∠C＝∠BAD；

(2)、求证：AC＝EF.

查看试题解析
22. 阅读：材料1：只含有一个未知数，并且未知数的最高次数是2次，最高次项的系数不为零，这样的整式方程叫做一元二次方程.一元二次方程有一种解法是利用因式分解来解的.如解方程：x²﹣3x+2＝0，左边分解因式得（x﹣1）（x﹣2）＝0，所以x﹣1＝0或x﹣2＝0，所以原方程的解是x＝1或x＝2.
材料2：立方和公式用字母表示为：x³+y³＝（x+y）（x²﹣xy+y²），

(1)、请利用材料1的方法解方程：x²﹣4x+3＝0；

(2)、请根据材料2类比写出立方差公式：x³﹣y³＝；（提示：可以用换元方法）

(3)、结合材料1和2，请你写出方程x⁶﹣7x³﹣8＝0所有根中的两个根.

查看试题解析
23. 某工厂计划在规定时间内生产24000个零件．若每天比原计划多生产30个零件，则在规定时间内可以多生产300个零件．

(1)、求原计划每天生产的零件个数和规定的天数

(2)、为了提前完成生产任务，工厂在安排原有工人按原计划正常生产的同时，引进5组机器人生产流水线共同参与零件生产，已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%．按此测算，恰好提前两天完成24000个零件的生产任务，求原计划安排的工人人数．

查看试题解析
24. 如图

(1)、问题探究：如图①，在四边形ABCD中，AB∥CD，E是BC的中点，AE是∠BAD的平分线，则线段AB，AD，DC之间的等量关系为；

(2)、方法迁移：如图②，在四边形ABCD中，AB∥CD，AF与DC的延长线交于点F，E是BC的中点，AE是∠BAF的平分线，试探究线段AB，AF，CF之间的等量关系，并证明你的结论；

(3)、联想拓展：如图③，AB∥CF，E是BC的中点，点D在线段AE上，∠EDF＝∠BAE，试探究线段AB，DF，CF之间的数量关系，并证明你的结论.

查看试题解析