湖北省黄石市大冶市2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2020-03-11 类型：期末考试

进入出卷网下载

一、单选题

1. 在以下“质量安全”，“回收”“绿色食品”“节水”四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 活动课上，老师给出长度分别是3cm，4cm，7cm，10cm的四根木棒，要求从中任选三根围成一个三角形，下面是四位同学分别选择的结果，你认为能围成三角形的是（）

A、3cm，4cm，7cm B、3cm，4cm，10cm C、3cm，7cm，10cm D、4cm，7cm，10cm

查看试题解析
3. 下列图形中有稳定性的是（）

A、正方形 B、长方形 C、直角三角形 D、平行四边形

查看试题解析
4. 下列分解因式中，完全正确的是（）

A、 $x^{3} - x = x (x^{2} - 1)$ B、 $4 a^{2} - 4 a + 1 = 4 a (a - 1) + 1$ C、 $x^{2} + y^{2} = {(x + y)}^{2}$ D、 $6 a - 9 - a^{2} = - {(a - 3)}^{2}$

查看试题解析
5. 英国曼彻斯特大学的两位科学家因为成功地从石墨中分离出石墨烯，荣获了诺贝尔物理学奖.石墨烯目前是世上最薄却也是最坚硬的纳米材料，同时还是导电性最好的材料，其理论厚度仅0.000 000 000 34米，将这个数用科学记数法表示为

A、 $0. 34 \times 1 0^{- 9}$ B、 $3 .4 \times 1 0^{- 9}$ C、 $3 .4 \times 1 0^{- 10}$ D、 $3 .4 \times 1 0^{- 11}$

查看试题解析
6. 如图，已知△ABC的六个元素，则下列甲、乙、丙三个三角形中和△ABC全等的图形是（）

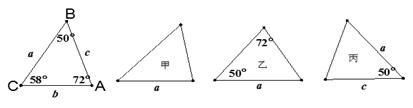A、甲 B、乙与丙 C、丙 D、乙

查看试题解析
7. 一个正多边形的每个外角都是36°，这个正多边形的边数是（）

A、9 B、10 C、11 D、12

查看试题解析
8. 张老师和李老师同时从学校出发，骑车去距学校20千米的县城购买书籍，张老师的汽车速度是李老师的1.5倍，结果张老师比李老师早到40分钟.设张老师骑车速度为x千米/小时，依题意，得到的方程是（）

A、 $\frac{20}{x} = \frac{20}{1.5 x} + \frac{2}{3}$ B、 $\frac{20}{x} = \frac{20}{1.5 x} - \frac{2}{3}$ C、 $\frac{20}{\frac{2}{3} x}$ ＝ $\frac{20}{x}$ ﹣ $\frac{2}{3}$ D、 $\frac{\frac{20}{2}}{3} x = \frac{20}{x} + \frac{2}{3}$

查看试题解析
9. 如图，DE是OABC中AC边的垂直平分线，若BC=8，AB=10，则△EBC的周长为（）

A、16 B、18 C、26 D、28

查看试题解析
10. 如图△ABC与△CDE都是等边三角形，且∠EBD=65°，则∠AEB的度数是（）

A、115° B、120° C、125° D、130°

查看试题解析

二、填空题

11. 当x为时，分式 $\frac{3 x - 6}{2 x + 1}$ 的值为0．

查看试题解析
12. 已知等腰三角形的两边长分别为3和5，则它的周长是．

查看试题解析
13. 一副分别含有30°和45°的两个直角三角板，拼成如图图形，其中∠C＝90°，∠B＝45°，∠E＝30°.则∠BFD的度数是.

查看试题解析
14. 已知 $\frac{x}{y}$ ＝2，则 $\frac{x^{2} - y^{2}}{x^{2} - 2 x y + y^{2}}$ 的值是.

查看试题解析
15. 已知关于x的方程 $\frac{x}{x - 3} - 2 = \frac{m}{x - 3}$ 有正数解，则m的取值是.

查看试题解析
16. 已知a²﹣4b＝﹣18，b²+10c＝7，c²﹣6a＝﹣27，则a+b+c的值是.

查看试题解析
17. 若关于x的方程 $\frac{2}{x - 2} + \frac{x + m}{2 - x} = 2$ 有增根，则m的值是

查看试题解析

三、解答题

18.

(1)、计算：（12a³﹣6a²）÷3a﹣2a（2a﹣1）；

(2)、解分式方程： $\frac{3}{2 x - 4} - \frac{x}{x - 2} =$ ＝1.

查看试题解析
19. 分解因式：

(1)、x²y﹣4y；

(2)、（a+2）（a﹣2）+3a.

查看试题解析
20. 先化简，再求值：1﹣ $\frac{a - b}{a + 2 b}$ ÷ $\frac{a^{2} - b^{2}}{a^{2} + 4 a b + 4 b^{2}}$ ，其中a=1，b=2．

查看试题解析
21. 如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．

(1)、求证：△ACD≌△AED；

(2)、若∠B=30°，CD=1，求BD的长．

查看试题解析
22. 作图题（不写作法）已知：如图，在平面直角坐标系中.

①作出△ABC关于y轴对称的△A₁B₁C₁ ，并写出△A₁B₁C₁三个顶点的坐标；

②求△ABC的面积；

③在x轴上画点P，使PA+PC最小.

查看试题解析
23. 如图①是我国古代数学家杨辉最早发现的，称为“杨辉三角”.它的发现比西方要早五百年左右，由此可见我国古代数学的成就是非常值得中华民族自豪的！

如图②是（a+b）ⁿ的三个展开式.结合上述两图之间的规律解题：

(1)、请直接写出（a+b）⁴的展开式：（a+b）⁴＝.

(2)、请结合图②中的展开式计算下面的式：（x+2）³＝.

查看试题解析
24. 某汽车销售公司经销某品牌A款汽车，随着汽车的普及，其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价2万元.如果卖出相同数量的A款汽车，去年销售额为100万元，今年销售额只有90万元.

(1)、今年5月份A款汽车每辆销售多少万元？

(2)、为了增加收入，汽车销售公司决定再经销同品牌的B款汽车，已知A款汽车每辆进价为8.5万元，B款汽车每辆进价为6万元，公司预计用多于100万元且少于110万元的资金购进这两款汽车共15辆，问有几种进货方案？

(3)、在（2）的前提下，如果B款汽车每辆售价为12万元，为打开B款汽车的销路，公司决定每售出一辆B款汽车，奖励顾客现金1.8万元，怎样进货公司的利润最大（假设能全部卖出）？最大利润是多少？

查看试题解析
25. 如图1，直线AB分别与x轴、y轴交于A、B两点，OC平分∠AOB交AB于点C，点D为线段AB上一点，过点D作DE//OC交y轴于点E，已知AO=m，BO=n，且m、n满足n²-12+36+|n-2m|=0.

(1)、求A、B两点的坐标?

(2)、若点D为AB中点，求OE的长?

(3)、如图2，若点P(x，-2x+6)为直线AB在x轴下方的一点，点E是y轴的正半轴上一动点，以E为直角顶点作等腰直角△PEF，使点F在第一象限，且F点的横、纵坐标始终相等，求点P的坐标.

查看试题解析