湖北省黄石市2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2020-03-11 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 以下运算正确的是（）

A、（ab³）²＝ab⁶ B、（﹣3xy）³＝﹣9x³y³ C、x³•x⁴＝x¹² D、（3x）²＝9x²

查看试题解析
3. 长方形的面积是9a²﹣3ab+6a³ ，一边长是3a，则它的另一边长是（）

A、3a²﹣b+2a² B、b+3a+2a² C、2a²+3a﹣b D、3a²﹣b+2a

查看试题解析
4. 化简 $\frac{m - 1}{m}$ ÷ $\frac{m - 1}{m^{2}}$ 的结果是（）

A、m B、 $\frac{1}{m}$ C、m－1 D、 $\frac{1}{m - 1}$

查看试题解析
5. 下列从左到右的变形中，属于因式分解的是（）

A、（x+1）（x﹣1）＝x²﹣1 B、x²﹣5x+6＝（x﹣2）（x﹣3） C、m²﹣2m﹣3＝m（m﹣2）﹣3 D、m（a+b+c）＝ma+mb+mc

查看试题解析
6. 已知a²+b²＝5，a﹣b＝1，则ab的值为（）

A、1 B、2 C、3 D、4

查看试题解析
7. 如图，等边三角形ABC中，AD⊥BC，垂足为D，点E在线段AD上，∠EBC=45°，则∠ACE等于（）

A、15° B、30° C、45° D、60°

查看试题解析
8. 一个多边形的每个内角都是108°，那么这个多边形是（）

A、五边形 B、六边形 C、七边形 D、八边形

查看试题解析
9. 角平分线的作法（尺规作图）
①以点O为圆心，任意长为半径画弧，交OA，OB于C，D两点；②分别以C，D为圆心，大于CD长为半径画弧，两弧交于点P；③过点P作射线OP，射线OP即为所求.

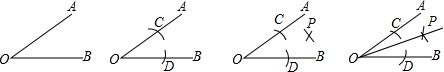
角平分线的作法依据的是（）

A、SSS B、SAS C、AAS D、ASA

查看试题解析
10. 如图，已知AC平分∠DAB，CE⊥AB于E，AB=AD+2BE，则下列结论：①AB+AD=2AE；②∠DAB+∠DCB=180°；③CD=CB；④S_△_ACE﹣2S_△_BCE=S_△_ADC；其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若分式 $\frac{x^{2} - 1}{x - 1}$ 的值为0，则x的值为.

查看试题解析
12. a，b，c为ΔABC的三边，化简|a-b-c|-|a+b-c|+2a结果是.

查看试题解析
13. 如图，AB=AC，BD=BC，若∠A=40°，则∠ABD的度数是.

查看试题解析
14. x $^{2}$ +4x+m是完全平方式，则m的值为.

查看试题解析
15. 计算: $2017 \times 2019 - 2018^{2} =$ .

查看试题解析
16. 若关于x的分式方程 $\frac{2}{x - 2} + \frac{m}{x^{2} - 4} = \frac{3}{x + 2}$ 无解，则m的值为.

查看试题解析

三、解答题

17. 计算

(1)、（x﹣3）（x+3）﹣6（x﹣1）²

(2)、a⁵•a⁴•a^﹣¹•b⁸+（﹣a²b²）⁴﹣（﹣2a⁴）²（b²）⁴

查看试题解析
18. 因式分解

(1)、16x⁴﹣1

(2)、3ax²+6axy+3ay²

查看试题解析
19. 解方程

(1)、 $\frac{1}{2 x} = \frac{2}{x + 3}$

(2)、 $\frac{x}{x - 1} = \frac{3}{2 x - 2}$ ﹣2

查看试题解析
20. 如图：AE=DE，BE=CE，AC和BD相交于点E，求证：AB=DC

查看试题解析
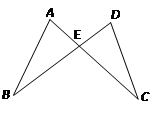21. 先化简，再求值： $(1 - \frac{1}{x - 1}) \div \frac{x^{2} - 4 x + 4}{x^{2} - 1}$ ，从 $- 1$ ，1，2，3中选择一个合适的数代入并求值.

查看试题解析
22. 已知△ABC，顶点A、B、C都在正方形方格交点上，正方形方格的边长为1.

(1)、写出A、B、C的坐标；

(2)、请在平面直角坐标系中画出△ABC关于x轴对称的△A₁B₁C₁；

(3)、在y轴上找到一点D，使得CD+BD的值最小，（在图中标出D点位置即可，保留作图痕迹）

查看试题解析
23. 甲、乙两人分别从距离目的地6千米和10千米的两地同时出发，甲、乙的速度比是3：4，结果甲比乙提前20分钟到达目的地，求甲、乙的速度.

查看试题解析
24. 如图1，△ABC中，AB＝AC，∠BAC＝90°，CD平分∠ACB，BE⊥CD，垂足E在CD的延长线上.请解答下列问题：

(1)、图中与∠DBE相等的角有：；

(2)、直接写出BE和CD的数量关系；

(3)、若△ABC的形状、大小不变，直角三角形BEC变为图2中直角三角形BED，∠E＝90°，且∠EDB＝ $\frac{1}{2}$ ∠C，DE与AB相交于点F.试探究线段BE与FD的数量关系，并证明你的结论.

查看试题解析
25. 在初中数学学习阶段，我们常常会利用一些变形技巧来简化式子，解答问题.
材料一：在解决某些分式问题时，倒数法是常用的变形技巧之一，所谓倒数法，即把式子变成其倒数形式，从而运用约分化简，以达到计算目的.

例：已知： $\frac{x}{x^{2} + 1} = \frac{1}{4}$ ，求代数式x²+ $\frac{1}{x^{2}}$ 的值.

解：∵ $\frac{x}{x^{2} + 1} = \frac{1}{4}$ ，∴ $\frac{x^{2} + 1}{x}$ ＝4

即 $\frac{x^{2}}{x} + \frac{1}{x}$ ＝4∴x+ $\frac{1}{x}$ ＝4∴x²+ $\frac{1}{x^{2}}$ ＝（x+ $\frac{1}{x}$ ）²﹣2＝16﹣2＝14

材料二：在解决某些连等式问题时，通常可以引入参数“k”，将连等式变成几个值为k的等式，这样就可以通过适当变形解决问题.

例：若2x＝3y＝4z，且xyz≠0，求 $\frac{x}{y + z}$ 的值.

解：令2x＝3y＝4z＝k（k≠0）

则 $x = \frac{k}{2} ， y = \frac{k}{3} ， z = \frac{k}{4} ， ∴ \frac{x}{y + z} = \frac{\frac{1}{2} k}{\frac{1}{3} k + \frac{1}{4} k} = \frac{\frac{1}{2}}{\frac{7}{12}} = \frac{6}{7}$

根据材料回答问题：

(1)、已知 $\frac{x}{x^{2} - x + 1} = \frac{1}{4}$ ，求x+ $\frac{1}{x}$ 的值.

(2)、已知 $\frac{a}{5} = \frac{b}{2} = \frac{c}{3}$ ，（abc≠0），求 $\frac{3 b + 4 c}{2 a}$ 的值.

(3)、若 $\frac{y z}{b z + c y} = \frac{z x}{c x + a z} = \frac{x y}{a y + b x} = \frac{x^{2} + y^{2} + z^{2}}{a^{2} + b^{2} + c^{2}}$ ，x≠0，y≠0，z≠0，且abc＝7，求xyz的值.

查看试题解析