湖北省恩施土家族苗族自治州咸丰县2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期：2020-03-11 类型：期末考试
一、单选题
-
1. 下列图形中不是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列图形中有稳定性的是（ ）A、正方形 B、长方形 C、直角三角形 D、平行四边形3. 在平面直角坐标系中，点P(﹣3，﹣5)关于y轴对称点的坐标为（ ）A、(﹣3，﹣5) B、(3，5) C、(3，﹣5) D、(5，﹣3)4. 下列计算正确的是（ ）A、x4•x3＝x12 B、（x3）4＝x81 C、（a+b）2＝a2+b2 D、（ab）2＝a2b25. 如图，已知AB＝AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）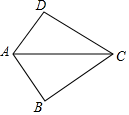
A、CB＝CD B、∠BCA＝∠DCA C、∠BAC＝∠DAC D、∠B＝∠D＝90°6. 下列说法错误的是（ ）A、三角形的高、中线、角平分线都是线段 B、三角形的三条中线都在三角形内部 C、锐角三角形的三条高一定交于同一点 D、三角形的三条高、三条中线、三条角平分线都交于同一点7. 要使分式 有意义，x的取值是（ ）A、x≠1 B、x≠﹣1 C、x≠±1 D、x≠±1且x≠﹣28. 小明同学把一个含有45°角的直角三角板在如图所示的两条平行线 m、n 上，测得 ，则 的度数是（ ）
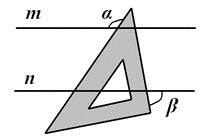A、45° B、55° C、65° D、75°9. 若m+n=3，则2m2+4mn+2n2﹣6的值为（ ）A、12 B、6 C、3 D、010. 若代数式 和 的值相等，则x的值为（ ）A、7 B、2 C、1 D、无解11. 如图所示，∠ABC＝∠ACB，CD⊥AC于C，BE⊥AB于B，AE交BC于点F，且BE＝CD，下列结论不一定正确的是（ ）
A、AB＝AC B、BF＝EF C、AE＝AD D、∠BAE＝∠CAD12. 如图，任意△ABC中，∠ABC与∠ACB的平分线交于点F，过点F作DE∥BC交AB于点D，交AC于点E，那么下列结论：①∠A＝2∠BFC﹣180°；②DE﹣BD＝CE；③△ADE的周长等于AB与AC的和；④BF＞CF.其中正确的有（ ）
A、① B、①② C、①②③ D、①②③④二、填空题
-
13. 计算：﹣（﹣2a2）2＝.14. ab＝2，a+b＝3，则（a﹣b）2＝.15. 如图，4个全等的长方形组成如图所示的图形，其中长方形的边长分别为a和b，且a＞b，求出阴影部分的面积为.
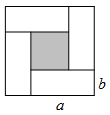16. 下面是一个三角形数阵
根据该数阵的规律，猜想第十行所有数的和.
三、解答题
-
17. 化简或计算下列各题(1)、 ；(2)、[（x+2）（x﹣2）]2.18. 解下列分式方程(1)、(2)、 .19. 将下列各式分解因式：(1)、（p﹣4）（p+1）+3p；(2)、4xy2﹣4x2y﹣y320. 如图，在平面直角坐标系中，直线l过点M（3，0），且平行于y轴.
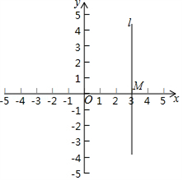
备用图
(1)、如果△ABC三个顶点的坐标分别是A（﹣2，0），B（﹣1，0），C（﹣1，2），△ABC关于y轴的对称图形是△A1B1C1 ， △A1B1C1关于直线l的对称图形是△A2B2C2 ， 写出△A2B2C2的三个顶点的坐标；(2)、如果点P的坐标是（﹣a，0），其中0＜a＜3，点P关于y轴的对称点是P1 ， 点P1关于直线l的对称点是P2 ， 求PP2的长.21. 先化简，再求值： ，其中x＝ .22. 某校为了丰富学生的校园生活，准备购进一批篮球和足球．其中篮球的单价比足球的单价多40元，用1500元购进的篮球个数与900元购进的足球个数相等．(1)、篮球和足球的单价各是多少元？(2)、该校打算用1000元购买篮球和足球，问恰好用完1000元，并且篮球、足球都买有的购买方案有哪几种？23. 已知：如图，△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，H是BC边的中点，连结DH与BE相交于点G.
(1)、求证：BF=AC；(2)、求证：CE= BF；(3)、CE与BG的大小关系如何？试证明你的结论.24. 如图，在直角坐标系中，长方形ABCD（每个内角都是90°）的顶点的坐标分别是A（0，m），B（n，0），（m＞n＞0），点E在AD上，AE＝AB，点F在y轴上，OF＝OB，BF的延长线与DA的延长线交于点M，EF与AB交于点N.
(1)、试求点E的坐标（用含m，n的式子表示）；(2)、求证：AM＝AN；(3)、若AB＝CD＝12cm，BC＝20cm，动点P从B出发，以2cm/s的速度沿BC向C运动的同时，动点Q从C出发，以vcm/s的速度沿CD向D运动，是否存在这样的v值，使得△ABP与△PQC全等？若存在，请求出v值；若不存在，请说明理由.