湖北省恩施土家族苗族自治州巴东县2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-03-11 类型:期末考试
一、单选题
-
1. 计算b•b2的结果是( )A、b3 B、b2 C、b D、12. 下列各式是分式的是( )A、 B、 C、 (a+b) D、3. 用科学计算法表示数0. 0012正确的是( )A、 B、 C、 D、4. 一个多边形的内角和等于 ,则它是( )边形A、7 B、8 C、9 D、105. 等边三角形的对称轴有( )条A、2 B、3 C、4 D、16. 等腰三角形一外角为 ,则底角的度数为( )A、 或 B、 C、 D、 或7. 下列变形中是因式分解的是( )A、 B、 C、 D、8. 已知4y2+my+9是完全平方式,则m为( )A、6 B、±6 C、±12 D、129. 下列等式成立的是( )A、(-3)-2=-9 B、(-3)-2= C、 =a14 D、 =-a2b610. 如图,已知点P到△ABC三边的距离相等,DE∥AC,AB=8.1cm,BC=6cm,△BDE的周长为( )cm
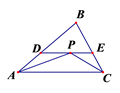 A、12 B、14.1 C、16.2 D、7.0511. 图中有三个正方形,若阴影部分面积为4个平方单位,则最大正方形的面积是( )平方单位.
A、12 B、14.1 C、16.2 D、7.0511. 图中有三个正方形,若阴影部分面积为4个平方单位,则最大正方形的面积是( )平方单位.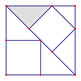 A、48 B、12 C、24 D、3612. 如图,AB=AC,∠A= ,AB的垂直平分线MN交AC于D,则∠DBC的度数( )
A、48 B、12 C、24 D、3612. 如图,AB=AC,∠A= ,AB的垂直平分线MN交AC于D,则∠DBC的度数( )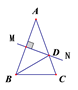 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 计算:(- ab2)3÷(-0.5a2b) =.14. 用乘法公式计算:[(x-2)(x+2)]2=.15. 如图,∠C=90°,∠A=30°,BD为角平分线,则SABD:S△CBD=.
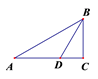 16. 若x=2019567891×2019567861,y=2019567881×2019567871,则xy(填>,<或=).
16. 若x=2019567891×2019567861,y=2019567881×2019567871,则xy(填>,<或=).三、解答题
-
17. 先化简,后求值.
1- ÷ ,其中a= ,b= .
18. 已知五边形ABCDE中,AB=AE,BC=DE,点F为CD的中点,∠B=∠E, 求证:AF⊥CD.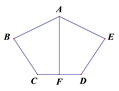 19. 甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件?20. x2+(p+q)x+pq型式子是数学学习中常见的一类多项式,如何将这种类型的式子因式分解呢?因为(x+p)(x+q)= x2+(p+q)x+pq,所以,根据因式分解是与整式乘法方向相反的变形,利用这种关系可得:x2+(p+q)x+pq=(x+p)(x+q).如:x2+3x+2=x2+(1+2)x+1×2=(x+1)(x+2),上述过程还可以形象的用十字相乘的形式表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项的系数,如下图.这样,我们可以得到:x2+3x+2= (x+1)(x+2),利用这种方法,将下列多项式分解因式:(1)、x2+7x+10(2)、-2x2-6x+36
19. 甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件?20. x2+(p+q)x+pq型式子是数学学习中常见的一类多项式,如何将这种类型的式子因式分解呢?因为(x+p)(x+q)= x2+(p+q)x+pq,所以,根据因式分解是与整式乘法方向相反的变形,利用这种关系可得:x2+(p+q)x+pq=(x+p)(x+q).如:x2+3x+2=x2+(1+2)x+1×2=(x+1)(x+2),上述过程还可以形象的用十字相乘的形式表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项的系数,如下图.这样,我们可以得到:x2+3x+2= (x+1)(x+2),利用这种方法,将下列多项式分解因式:(1)、x2+7x+10(2)、-2x2-6x+36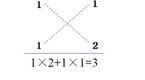 21. 在日历上我们可以发现其中某些数满足一定的规律.如图是2018年8月份的日历,我们任意选择其中所示的方框部分,将方框部分中的4个位置的数交叉相乘,再相减,如8×16-9×15=-7,19×27-20×26=-7,不难发现结果都是-7.
21. 在日历上我们可以发现其中某些数满足一定的规律.如图是2018年8月份的日历,我们任意选择其中所示的方框部分,将方框部分中的4个位置的数交叉相乘,再相减,如8×16-9×15=-7,19×27-20×26=-7,不难发现结果都是-7.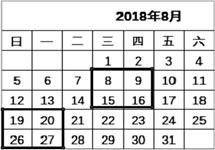 (1)、请你再选择一组数按上面的方式计算,看看是否符合这个规律.并用你擅长的表达方式描述这个规律.(2)、请你利用整式的运算对以上的规律加以证明.22.(1)、如图,AE是∠MAD的平分线,点C是AE上一点,点B是AM上一点,在AD上求作一点P,使得△ABC≌△APC,请保留清晰的作图痕迹.
(1)、请你再选择一组数按上面的方式计算,看看是否符合这个规律.并用你擅长的表达方式描述这个规律.(2)、请你利用整式的运算对以上的规律加以证明.22.(1)、如图,AE是∠MAD的平分线,点C是AE上一点,点B是AM上一点,在AD上求作一点P,使得△ABC≌△APC,请保留清晰的作图痕迹.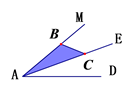 (2)、如图a,在△ABC中, ∠ACB= 90°,∠A= 60°,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.请探究线段BC、BF、CE之间的关系,直接写出结论,不要求证明.
(2)、如图a,在△ABC中, ∠ACB= 90°,∠A= 60°,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.请探究线段BC、BF、CE之间的关系,直接写出结论,不要求证明.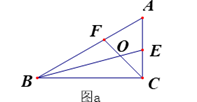 (3)、如图b,若(2)中∠ACB为任意角,其它条件不变,请探究BC、BF、CE之间又有怎样的关系,请证明你的结论.
(3)、如图b,若(2)中∠ACB为任意角,其它条件不变,请探究BC、BF、CE之间又有怎样的关系,请证明你的结论.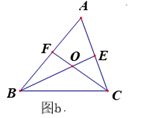 23. 如图a,网格中的每一个正方形的边长为1,△ABC为格点三角形,直线MN为格点直线(点A、B、C、M、N在小正方形的顶点上).
23. 如图a,网格中的每一个正方形的边长为1,△ABC为格点三角形,直线MN为格点直线(点A、B、C、M、N在小正方形的顶点上).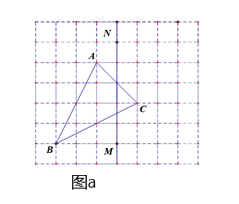 (1)、仅用直尺在图a中作出△ABC关于直线MN的对称图形△A′B′C′.(2)、如图b,仅用直尺将网格中的格点三角形ABC的面积三等分,并将其中的一份用铅笔涂成阴影.
(1)、仅用直尺在图a中作出△ABC关于直线MN的对称图形△A′B′C′.(2)、如图b,仅用直尺将网格中的格点三角形ABC的面积三等分,并将其中的一份用铅笔涂成阴影.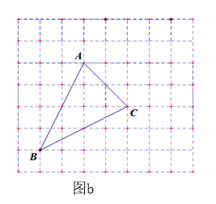 (3)、如图c,仅用直尺作三角形ABC的边AC上的高,简单说明你的理由.
(3)、如图c,仅用直尺作三角形ABC的边AC上的高,简单说明你的理由.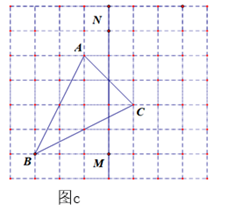 24. 如图a,P、Q是△ABC的边BC上的两点,且△APQ为等边三角形,AB=AC,
24. 如图a,P、Q是△ABC的边BC上的两点,且△APQ为等边三角形,AB=AC,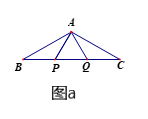
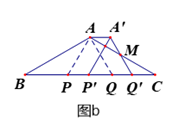 (1)、求证:BP=CQ.(2)、如图a,若∠BAC=120 ,AP=3,求BC的长.(3)、若∠BAC=120 ,沿直线BC向右平行移动△APQ得到△A′P′Q′(如图b),A′Q′与AC交于点M.当点P移动到何处时,△AA′M≌△CQ′M?证明你的结论.
(1)、求证:BP=CQ.(2)、如图a,若∠BAC=120 ,AP=3,求BC的长.(3)、若∠BAC=120 ,沿直线BC向右平行移动△APQ得到△A′P′Q′(如图b),A′Q′与AC交于点M.当点P移动到何处时,△AA′M≌△CQ′M?证明你的结论.