河南省周口市鹿邑县2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2020-03-11 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 正六边形的外角和是（）

A、 $360^{\circ}$ B、 $540^{\circ}$ C、 $720^{\circ}$ D、 $60^{\circ}$

查看试题解析
3. 目前我国能制造芯片的最小工艺水平已达到7纳米，居世界前列，在 $5 G$ 时代赢得了一席之地，已知1纳米=0.000000001米，用科学记数法将7纳米表示为（）

A、 $0.7 \times 10^{- 8}$ B、 $70 \times 10^{-10}$ C、 $7 \times 10^{-9}$ D、 $7 \times 10^{-10}$

查看试题解析
4. 下列运算正确的是（）

A、 $b^{5} \div b^{3} = b^{2}$ B、 ${(b^{5})}^{2} = b^{7}$ C、 $b^{2} \cdot b^{4} = b^{8}$ D、 $a \cdot （ a - 2 b ） = a^{2} + 2 a b$

查看试题解析
5. 点P在∠AOB的平分线上，点P到OA边的距离等于5，点Q是OB边上的任意一点，则下列选项正确的是（）

A、PQ≤5 B、PQ<5 C、PQ≥5 D、PQ>5

查看试题解析
6. 不改变分式 $\frac{0.5 x - 1}{0.3 x + 2}$ 的值，把分子和分母中各项的系数都化为整数，则所得的结果为（）

A、 $\frac{5 x - 1}{3 x + 2}$ B、 $\frac{5 x - 10}{3 x + 20}$ C、 $\frac{2 x - 1}{3 x + 2}$ D、 $\frac{x - 2}{3 x + 20}$

查看试题解析
7. 分解因式 $x^{3} y - 2 x^{2} y^{2} + x y^{3}$ 正确的是（）

A、 $x y {(x + y)}^{2}$ B、 $x y (x^{2} - 2 x y + y^{2})$ C、 $x y (x^{2} + 2 x y - y^{2})$ D、 $x y {(x - y)}^{2}$

查看试题解析
8. 如图，已知 $Δ A B E ≅ Δ A C D$ ，若 $∠ B = 50^{\circ}$ ， $∠ A E C = 120^{\circ}$ ，则 $∠ D A C$ 的度数为（）

A、 $120^{\circ}$ B、 $70^{\circ}$ C、 $60^{\circ}$ D、 $50^{\circ}$

查看试题解析
9. 已知等腰三角形的其中两边长分别为4，9，则这个等腰三角形的周长是（）

A、13 B、17 C、22 D、17或22

查看试题解析
10. 小玲每天骑自行车或坐公交车上学，她上学的路程为20千米，坐公交车的平均速度是骑自行车的平均速度的3倍，坐公交车比骑自行车上学早到40分钟，设小玲骑自行车的平均速度为 $x$ 千米/小时，根据题意，下面列出的方程正确的是（）

A、 $\frac{20}{x} - \frac{20}{3 x} = 40$ B、 $\frac{20}{3 x} - \frac{20}{x} = 40$ C、 $\frac{20}{x} - \frac{20}{3 x} = \frac{2}{3}$ D、 $\frac{20}{3 x} - \frac{20}{x} = \frac{2}{3}$

查看试题解析

二、填空题

11. 若分式 $\frac{x - 2}{x}$ 的值是0，则x的值为．

查看试题解析
12. ${(2 x + 1)}^{2} =$ .

查看试题解析
13. 如图， $Δ A B C$ 与 $Δ D C E$ 都是等边三角形， $B ， C ， E$ 三点在同一条直线上，若 $A B = 3$ ， $∠ B A D = 150^{\circ}$ ，则 $D E$ 的长为.

查看试题解析
14. 如图，小志同学将边长为3的正方形塑料模板 $A B C D$ 与一块足够大的直角三角板叠放在一起，其中直角三角板的直角顶点落在点 $A$ 处，两条直角边分别与 $C D$ 交于点 $F$ ，与 $C B$ 延长线交于点 $E$ ，则四边形 $A E C F$ 的面积是.

查看试题解析
15. 若关于 $x$ 的分式方程 $\frac{6}{x - 1} = \frac{x + 3}{x (x - 1)} - \frac{k}{x}$ 无解，则 $k$ 的值为.

查看试题解析

三、解答题

16. 解方程： $\frac{2 x}{2 x - 1} + \frac{5}{1 - 2 x}$ ＝3.

查看试题解析
17. 计算： $[(x y + 2) (x y - 2) - 2 x^{2} y^{2} + 4] \div x y$

查看试题解析
18. 如图，在平面直角坐标系中， $Δ A B C$ 的顶点坐标为 $A (- 2 ， 4)$ ， $B (- 4 ， 1)$ ， $C (- 1 ， 1)$ .

(1)、作出 $Δ A B C$ 关于 $x$ 轴对称图形 $Δ A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ ， $C_{1}$ 的坐标

(2)、求 $Δ A_{1} B_{1} C_{1}$ 的面积.

查看试题解析
19. 如图，在 $Δ A B C$ 中， $∠ A B C = ∠ A C B$ ， $∠ A = 50^{\circ}$ ， $P$ 是 $Δ A B C$ 内一点，且 $∠ P B C = ∠ P C A$ ，求 $∠ B P C$ .

查看试题解析
20. 先化简再求值： $(1 - \frac{1}{x - 1}) \div \frac{x^{2} - 4}{x^{2} + 4 x + 4}$ ，其中 $x = 2$ .

查看试题解析
21. 如图，已知四边形ABCD是梯形，AD∥BC，∠A＝90°，BC＝BD，CE⊥BD，垂足为E．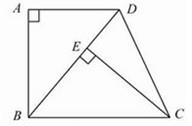

(1)、求证：△ABD≌△ECB；

(2)、若∠DBC＝50°，求∠DCE的度数．

查看试题解析
22. 某学校计划从商店购进 $A, B$ 两种商品，购买一个 $A$ 商品比购买一个 $B$ 商品多花10元，并且花费300元购买 $A$ 商品和花费100元购买 $B$ 商品的数量相等.

(1)、求购买一个 $A$ 商品和一个 $B$ 商品各需要多少元；

(2)、根据学校实际情况，该学校需要购买 $B$ 种商品的个数是购买 $A$ 种商品个数的3倍，还多11个，经与商店洽谈，商店决定在该学校购买 $A$ 种商品时给予八折优惠，如果该学校本次购买 $A, B$ 两种商品的总费用不超过1000元，那么该学校最多可购买多少个 $A$ 种商品？

查看试题解析
23. $Δ A B C$ 与 $Δ D C E$ 有公共顶点 $C$ （顶点均按逆时针排列）， $A B = A C$ ， $D C = D E$ ， $∠ B A C + ∠ C D E = 180 °$ ， $D E / / B C$ ，点 $G$ 是 $B E$ 的中点，连接 $D G$ 并延长交直线 $B C$ 于点 $F$ ，连接 $A F ， A D$ .

(1)、如图，当 $∠ B A C = 90 °$ 时，
求证：① $B F = C D$ ；

② $Δ A F D$ 是等腰直角三角形.

(2)、当 $∠ B A C = 60 °$ 时，画出相应的图形（画一个即可），并直接指出 $Δ A F D$ 是何种特殊三角形.

查看试题解析