江苏省连云港市灌云县西片2018-2019学年七年级下学期数学第一次月考试卷
试卷更新日期：2020-03-11 类型：月考试卷
一、单选题
-
1. 下列计算正确的是（ ）A、y7•y＝y8 B、b4﹣b4＝1 C、x5+x5＝x10 D、a3×a2＝a62. 某细胞的直径约为 米，该直径用科学记数法表示为A、 米 B、 米 C、 米 D、 米3. 若一个多边形的内角和是1080°，则此多边形的边数是（ ）A、十二 B、十 C、八 D、十四4. 在△ABC中，∠A是钝角，下列图中画BC边上的高线正确的是（ ）A、
B、
C、
D、
5. 如图，把一张长方形的纸片ABCD沿EF折叠，若∠AED′＝40°，则∠DEF的度数为（ ）
A、40° B、50° C、60° D、70°6. 如图在一块长为12m，宽为6m的长方形草地上，有一条弯曲的柏油小路（小路任何地方的水平宽度都是2m）则空白部分表示的草地面积是（ ）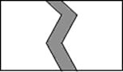
A、70 B、60 C、48 D、187. 如图，已知△ABC中，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（ ）
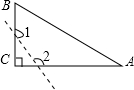A、90° B、135° C、270° D、315°8. 如图，已知△ABC的内角∠A=α，分别作内角∠ABC与外角∠ACD的平分线，两条平分线交于点A1 ， 得∠A1；∠A1BC和∠A1CD的平分线交于点A2 ， 得∠A2；…以此类推得到∠A2017 ， 则∠A2017的度数是（ ）
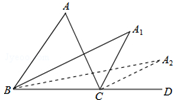A、 α B、90+ α C、 α D、 α二、填空题
-
9. 计算：（﹣2a3）2= ．10. 已知△ABC中，AB＝2，BC＝5，且AC的长为偶数，则AC的长为.11. 将a=（﹣99）0 ， b=（﹣0.1）﹣1 ， ，这三个数从小到大的顺序排为 ．12. 如图，条件（填写所有正确的序号）一定能判定AB∥CD.
①∠B+∠BCD=180°；②∠1=∠2；③∠3=∠4；④∠B=∠5.
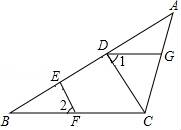
13. 如图，在△ABC中，已知D，E，F分别为边BC，AD，CE的中点，且 ，则阴影部分的面积为 cm2.
14. 小明从点O出发，前进5m后向右转15°，再前进5米后向右转15°，…一直这样走下去，直到他第一次回到出发点O为止，他所走的路径构成了一个多边形，小明走的路程总和是米.
15. （﹣4）2019•（﹣0.25）2018=.16. 如图所示，第1个图案是由黑白两种颜色的六边形地面砖组成的，第2个，第3个图案可以看成是第1个图案经过平移而得：那么第2019个图案中有白色六边形地面砖块.
三、解答题
-
17. 计算：(1)、﹣30﹣2﹣3+( )﹣1(2)、(﹣a3)2•a3﹣(﹣3a3)318. 一个多边形的内角和比外角和的3倍少180°.求：(1)、这个多边形的边数；(2)、该多边形共有多少条对角线.19. 如图，在6×6的正方形网格中，每个小正方形的边长为1，点A、B、C、D、E、F、M、N、P均为格点(格点是指每个小正方形的顶点).
(1)、利用图①中的网格，过P点画直线MN的平行线和垂线.(2)、把图②网格中的三条线段AB、CD、EF通过平移使之首尾顺次相接组成一个三角形(在图②中画出三角形).(3)、第(2)小题中线段AB、CD、EF首尾顺次相接组成一个三角形的面积是.20.(1)、已知2x=3，2y=5，求2x+y的值；(2)、x﹣2y+1=0，求：2x÷4y×8的值.21.在△ABC中，CD⊥AB于D，CE是∠ACB的平分线，∠A=20°，∠B=60°．求∠BCD和∠ECD的度数．
22. 如图，AD平分∠EAC，若∠C=55°，∠EAC=110°，AD与BC平行吗？为什么？请根据解答过程填空（理由或数学式）
解：AD∥BC.理由：
∵AD平分∠EAC（已知）
∴∠DAC= ∠EAC（）
∵∠EAC=110°（已知）
∴∠DAC= ∠EAC=°
∵∠C=55°（已知）
∴∠C=∠
∴AD∥BC（）
23. 比较2100与375的大小.24. 如图所示，在△ABC中，D是BC边上一点∠1＝∠2，∠3＝∠4，∠BAC＝69°，求∠DAC的度数．
25. 规定两数a、b之间的一种运算，记作（a，b）：如果 ，那么（a，b）=c.例如：因为 ，所以（2，8）=3.
(1)、根据上述规定，填空：（5，125）= ， （-2，4）= ， （-2，-8）=；
(2)、小明在研究这种运算时发现一个现象： ，他给出了如下的证明：设 ，则 ，即
∴ ，即 ，
∴ .
请你尝试运用上述这种方法说明下面这个等式成立的理由.
(4，5)＋(4，6)=(4，30)
