江苏省丹阳市吕城片2018-2019学年七年级下学期数学第一次月考试卷
试卷更新日期:2020-03-11 类型:月考试卷
一、单选题
-
1. 观察下列图案,在A,B,C,D四幅图案中,能通过图案(1)平移得到的是…( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 如果一个三角形的两条边长分别为2和6,那么这个三角形第三边的长可能是 ( )A、2 B、3 C、4 D、6.24. 多边形内角和的度数可能为 ( )A、240° B、360° C、480° D、520°5. 三角形的三条高线的交点在三角形的一个顶点上,则此三角形是( )A、等腰三角形 B、锐角三角形 C、直角三角形 D、钝角三角形6.
2. 下列计算正确的是( )A、 B、 C、 D、3. 如果一个三角形的两条边长分别为2和6,那么这个三角形第三边的长可能是 ( )A、2 B、3 C、4 D、6.24. 多边形内角和的度数可能为 ( )A、240° B、360° C、480° D、520°5. 三角形的三条高线的交点在三角形的一个顶点上,则此三角形是( )A、等腰三角形 B、锐角三角形 C、直角三角形 D、钝角三角形6.如图,下列判断正确的是( )
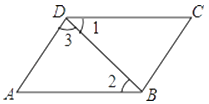 A、若∠1=∠2,则AD∥BC B、若∠1=∠2,则AB∥CD C、若∠A=∠3,则AD∥BC D、若∠A+∠ADC=180°,则AD∥BC7. 将边长为1的一个正方形和一个等边三角形按如图的方式摆放,则 的面积为( )
A、若∠1=∠2,则AD∥BC B、若∠1=∠2,则AB∥CD C、若∠A=∠3,则AD∥BC D、若∠A+∠ADC=180°,则AD∥BC7. 将边长为1的一个正方形和一个等边三角形按如图的方式摆放,则 的面积为( ) A、1 B、 C、 D、8. 如图,三角形 内的线段 相交于点 ,已知 , .若 的面积=2,则四边形 的面积等于( )
A、1 B、 C、 D、8. 如图,三角形 内的线段 相交于点 ,已知 , .若 的面积=2,则四边形 的面积等于( ) A、4 B、5 C、6 D、7
A、4 B、5 C、6 D、7二、填空题
-
9. 计算: , , .10. 比较大小: .11. 若△ABC中,∠A:∠B:∠C=2:3:4,则△ABC是 三角形.(填:锐角或直角或钝角)12. 如图AD⊥BD,AE平分∠BAC,∠ACD=70°,∠B=30°.则∠DAE的度数为°.
 13. 如图,小明在操场上从A点出发,沿直线前进15米后向左转45°,再沿直线前进150米后,又向左转45°,照这样走下去,他第一次回到出发地A点时,一共走了米.
13. 如图,小明在操场上从A点出发,沿直线前进15米后向左转45°,再沿直线前进150米后,又向左转45°,照这样走下去,他第一次回到出发地A点时,一共走了米. 14. 等腰三角形两边长分别为5,7,则其周长为.15. 如图,三角形ABE向右平移一定距离后得到三角形CDF,若∠BAE=60º,∠B=25º,则∠ACD=.
14. 等腰三角形两边长分别为5,7,则其周长为.15. 如图,三角形ABE向右平移一定距离后得到三角形CDF,若∠BAE=60º,∠B=25º,则∠ACD=. 16. 某小区门口的曲臂道闸如图所示,BA垂直地面AE于点A,横杆CD平行于地面AE,则∠ABC+∠BCD=度.
16. 某小区门口的曲臂道闸如图所示,BA垂直地面AE于点A,横杆CD平行于地面AE,则∠ABC+∠BCD=度.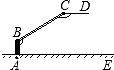 17. 如图,在第1个 中, 40°, ,在 上取一点 ,延长 到 ,使得在第2个 中, ;在 上取一点 ,延长 到 ,使得在第3个 中, ;…,按此做法进行下去,第3个三角形中以 为顶点的内角的度数为; 第 个三角形中以 为顶点的内角的度数为度.
17. 如图,在第1个 中, 40°, ,在 上取一点 ,延长 到 ,使得在第2个 中, ;在 上取一点 ,延长 到 ,使得在第3个 中, ;…,按此做法进行下去,第3个三角形中以 为顶点的内角的度数为; 第 个三角形中以 为顶点的内角的度数为度. 18. 如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.
18. 如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°. (1)、将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;(2)、将图①中的三角板OMN绕点O按逆时针方向旋转至如图③,当∠CON=5∠DOM时,MN与CD相交于点E,请你判断MN与BC的位置关系,并求∠CEN的度数;(3)、将图①中的三角板OMN绕点O按每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,三角板MON运动几秒后直线MN恰好与直线CD平行.(4)、将如图①位置的两块三角板同时绕点O逆时针旋转,速度分别每秒20°和每秒10°,当其中一个三角板回到初始位置时,两块三角板同时停止转动.经过秒后边OC与边ON互相垂直.(直接写出答案)
(1)、将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;(2)、将图①中的三角板OMN绕点O按逆时针方向旋转至如图③,当∠CON=5∠DOM时,MN与CD相交于点E,请你判断MN与BC的位置关系,并求∠CEN的度数;(3)、将图①中的三角板OMN绕点O按每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,三角板MON运动几秒后直线MN恰好与直线CD平行.(4)、将如图①位置的两块三角板同时绕点O逆时针旋转,速度分别每秒20°和每秒10°,当其中一个三角板回到初始位置时,两块三角板同时停止转动.经过秒后边OC与边ON互相垂直.(直接写出答案)三、解答题
-
19. 计算(1)、(2)、20. 已知 , ,求 3×9m×27n 的值.


