湖北省武汉市蔡甸区12校2018-2019学年七年级下学期数学3月月考试卷
试卷更新日期：2020-03-11 类型：月考试卷
一、单选题
-
1. 下列各式正确的是（ ）A、± ＝0.6 B、 =±3 C、 = D、 =-a2. 已知y= + -3，那么yx的值是（ ）
A、-6 B、-9 C、6 D、93. 下列条件不能判定AB//CD的是（ ）
A、∠3=∠4 B、∠1=∠5 C、∠1+∠2=180° D、∠3=∠54. 下列说法：①若a与c相交，b与c相交，则a与b相交；②若a//b，b//c，那么a//c；③经过直线外一点有且只有一条直线与已知直线平行；④两条直线的位置关系有平行与相交.
其中错误的说法有（ ）
A、3个 B、2个 C、1个 D、0个5. 平面内有三条直线，那么它们的交点个数有（ ）A、0个或1个 B、0个或2个 C、0个或1个或2个 D、0个或1个或2个或3个6. 如图，CD//AB，AC⊥BC，∠ACD=60°，那么∠B的度数是（ ）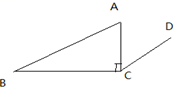
A、60° B、40° C、45° D、30°7. 如图，如果AB∥CD，CD∥EF，那么∠BCE等于（ ）
A、∠1+∠2 B、∠2﹣∠1 C、180°﹣∠2+∠1 D、180°﹣∠1+∠28. 若∠A的两边与∠B的两边分别平行，且3∠A－∠B=80°，那么∠B的度数为（ ）A、80°或100° B、65°或115° C、40°或140° D、40°或115°9. 如图，三组互相垂直的线段，已知AD=2，BC=8，BF=4，那么AC的长度等于（ ）
A、2 B、3 C、4 D、510. 如图，AF∥CD，BC平分∠ACD，BD平分∠EBF，且BC⊥BD.下列结论：①BC平分∠ABE；②AC∥BE；③∠BCD+∠D=90°；④∠DBF=2∠ABC．其中正确的个数为（ ）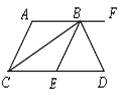
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. = ， │π-4│= ， 若a>b，c<0则-2ac-2bc（填>或<）12. 表示一个整数，那么表示n的最小正整数是.13. 若 +|1﹣a|＝a+3，则a＝.14. 实数a的位置如图所示，那么a 、－a、 、a2的大小关系是.
15. 已知x、y、z满足 = = ，那么 ＝.16. 已知∠A与∠B的两边一边平行，另一边垂直，∠A=x°，那么∠B等于.三、解答题
-
17. 计算：(1)、 + - - ( ) 2(2)、│ - │+218. 求下列各式中x的值.(1)、4 (x-1) 2=25(2)、 (x+2) 2=719. 如图，已知△ABC，按要求作图.
(1)、①过点A作BC的垂线段AD；②过C作AB、AC的垂线分别交AB于点E、F；
(2)、AB=15，BC=7，AC=20，AD=12，求点C到线段AB的距离.20. 完成下面的推理：如图，已知DE⊥BC于E、FG⊥BC于G，∠1=∠2.求证：EH//AC.
证明：延长HE、FG相交于点Q.
∵DE⊥BC FG⊥BC （已知）
∴∠DEC=90°，∠FGC=90°（）
∴∠DEC=∠FGC（）
∴DE//（）
∴∠1=（）
又 ∠1=∠2 （已知）
∴ ∠2=（等量代换）
∴ EH//AC（）
21. 如图，在△ABC中，∠1=∠2，ED//BC，CD⊥AB于点D.求证：∠FGB=90°.
22. 如图，用两个边长为15 cm的小正方形拼成一个大的正方形.
(1)、求大正方形的边长？(2)、若沿此大正方形边的方向剪出一个长方形，能否使剪出的长方形纸片的长宽之比为4：3且面积为720cm2.若能，试求出剪出的长方形纸片的长与宽；若不能，试说明理由？
