江苏省兴化市顾庄学区2018-2019学年八年级下学期数学第一次月考试卷

试卷更新日期：2020-03-11 类型：月考试卷

进入出卷网下载

一、单选题

1. 若 $\frac{1}{x - 3}$ 有意义，则x的取值范围是（）

A、x＞3 B、x＜3 C、x≠﹣3 D、x≠3

查看试题解析
2. 化简 $\frac{a^{2} + 3 a}{a + 3}$ 的结果是（）

A、﹣3 B、3 C、﹣a D、a

查看试题解析
3. 菱形不具备的性质是（）

A、四条边都相等 B、对角线一定相等 C、是轴对称图形 D、是中心对称图形

查看试题解析
4. 如果解分式方程 $\frac{x}{x - 3} = \frac{3}{x - 3}$ 出现了增根，那么增根是（）

A、0 B、-1 C、3 D、1

查看试题解析
5. 下列分式是最简分式的是（）

A、 $\frac{2 a - 4}{2 a + 6}$ B、 $\frac{b + 1}{a b + a}$ C、 $\frac{a + b}{a^{2} - b^{2}}$ D、 $\frac{a + b}{a^{2} + b^{2}}$

查看试题解析
6. 已知平行四边形ABCD，下列条件中，不能判定这个平行四边形为矩形的是（）

A、∠A=∠B B、∠A=∠C C、AC=BD D、AB⊥BC

查看试题解析

二、填空题

7. 若分式 $\frac{x - 4}{x}$ 的值为0，则x的值是.

查看试题解析
8. 化简： $\frac{a b + b^{2}}{b}$ ＝.

查看试题解析
9. 计算： $\frac{2}{x - 3} + \frac{1}{3 - x}$ ＝．

查看试题解析
10. 计算： $\frac{1}{a - 2} \div \frac{a}{a^{2} - 4}$ =.

查看试题解析
11. 如图，在△ABC中，AB＝6，BC＝7，AC＝10.点D、E、F分别是相应边上的中点，则四边形DEBF的周长等于.

查看试题解析
12. 如图，矩形ABCD的两条对角线相交于点O，若∠AOB＝60°，AB＝3，则BD＝.

查看试题解析
13. 已知关于x的方程 $\frac{2 x + m}{x - 3}$ ＝3的解是非负数，则m的取值范围是.

查看试题解析
14. 已知x²﹣4x﹣5＝0，则分式 $\frac{6 x}{x^{2} - x - 5}$ 的值是.

查看试题解析
15. 如图，在正方形ABCD中，点H，E，G，F分别在AB，BC，CD，DA上，若EF⊥HG于点O，若AB=12，EF=13，H为AB的中点，则DG＝.

查看试题解析

三、解答题

16. 计算：

(1)、 $- a + \frac{a^{2}}{a - 1}$

(2)、 $\frac{x^{2}}{x + 1} - x + 1$

查看试题解析
17. 化简：

(1)、 $\frac{x + 1}{x^{2} - 1} \cdot \frac{x^{2} - 2 x + 1}{x^{2} - x}$

(2)、 $\frac{a - 2}{a + 3}$ ÷ $\frac{a^{2} - 4}{2 a + 6}$ - $\frac{5}{a + 2}$

查看试题解析
18. 解方程：

(1)、 $\frac{2}{x}$ + $\frac{x}{x - 2}$ ＝1

(2)、 $\frac{x}{x + 3} = 1 - \frac{x - 1}{x^{2} - 9}$

查看试题解析
19. 先化简，再求值： $\frac{a^{2} + a}{a^{2} - 2 a + 1} \div (\frac{2}{a - 1} - \frac{1}{a})$ ，其中a²+a﹣1＝0.

查看试题解析
20. 南京到上海铁路长360km,为了适应两市经济的发展,某客运列车的行驶速度增加到原来的1.5倍,因此从南京到上海的时间缩短了1小时,求客运列车原来的速度.

查看试题解析
21. 如图，BD是△ABC的角平分线，过点D作DE∥BC交AB于点E，DF∥AB交BC于点F.

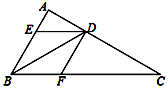(1)、求证：四边形BEDF为菱形；

(2)、如果∠A＝100°，∠C＝30°，求∠BDE的度数.

查看试题解析
22.

(1)、已知a²-3a+1=0，求a²+ $\frac{1}{a^{2}}$ 的值

(2)、已知A＝ $\frac{1}{a + 1} + \frac{1}{b + 1}$ ，B＝ $\frac{a}{a + 1} + \frac{b}{b + 1}$ ，若A＝B，求a、b之间的关系式；

查看试题解析
23. 如图，在矩形ABCD中，AC，BD交于点O，延长BC到点E，使CE＝BC，连接AE交CD于点F.

(1)、求证：OF//BE.

(2)、若OD=5，BC=6，求△AOF的面积.

查看试题解析
24. 探究:

(1)、若 $\frac{x - 1}{x + 1}$ =1+ $\frac{a}{x + 1}$ ,试求a的值.

(2)、若 $\frac{x^{2}}{x - 2}$ = x+2+ $\frac{b}{x - 2}$ ,试求b的值.

(3)、如果分式 $\frac{2 x^{2} - 7}{x - 2}$ 的值为整数,求x的整数值.

查看试题解析
25. 如图，正方形ABCD的顶点A在等腰直角△DFG的斜边FG上，FG与BC相交于点E，连接CF.

(1)、求证：△DAG≌△DCF；

(2)、连结BD交AF于H，若∠BHE=65°，求∠FDC的度数.

(3)、在（2）的条件下，试探究线段GA，AH，FH之间的特殊数量关系，并说明理由.

查看试题解析