江苏省如皋市2018-2019学年八年级下学期数学第一次月考试卷
试卷更新日期:2020-03-11 类型:月考试卷
一、单选题
-
1.
如图,要使▱ABCD成为菱形,则需添加的一个条件是( )
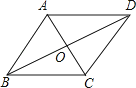 A、AC=AD B、BA=BC C、∠ABC=90° D、AC=BD2. 函数y= + 中自变量x的取值范围是( )
A、AC=AD B、BA=BC C、∠ABC=90° D、AC=BD2. 函数y= + 中自变量x的取值范围是( )
A、x≤2 B、x≤2且x≠1 C、x<2且x≠1 D、x≠13. 菱形具有而平行四边形不具有的性质是( )A、两组对边分别平行 B、两组对角分别相等 C、对角线互相平分 D、对角线互相垂直4. 下列四个图象中,不表示某一函数图象的是( )
A、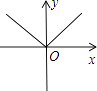 B、
B、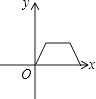 C、
C、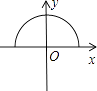 D、
D、 5. 如图,在▱ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,▱ABCD的周长是在14,则DM等于( )
5. 如图,在▱ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,▱ABCD的周长是在14,则DM等于( )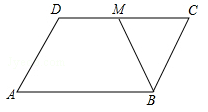 A、1 B、2 C、3 D、46. 如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2km,则M、C两点间的距离为( )
A、1 B、2 C、3 D、46. 如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2km,则M、C两点间的距离为( )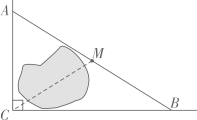 A、0.5km B、0.6km C、0.9km D、1.2km7. 如图所示,在△ABC中,M是BC的中点,AN平分∠BAC,BN⊥AN.若AB=14,AC=20,则MN的长为( )
A、0.5km B、0.6km C、0.9km D、1.2km7. 如图所示,在△ABC中,M是BC的中点,AN平分∠BAC,BN⊥AN.若AB=14,AC=20,则MN的长为( )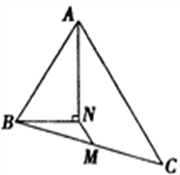 A、2 B、2.5 C、3 D、3.58. 如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A﹣B﹣C﹣O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
A、2 B、2.5 C、3 D、3.58. 如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A﹣B﹣C﹣O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )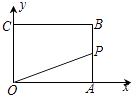 A、
A、 B、
B、 C、
C、 D、
D、 9. 如图, 是 内一点, , , , , 、 、 、 分别是 、 、 、 的中点,则四边形 的周长是( )
9. 如图, 是 内一点, , , , , 、 、 、 分别是 、 、 、 的中点,则四边形 的周长是( )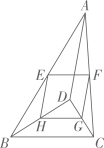 A、 B、 C、 D、10. 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
A、 B、 C、 D、10. 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若平行四边形中两个内角的度数比为1:2,则其中较大的内角是 度.12. 已知菱形的两条对角线长分别是6和8,则这个菱形的面积为 .13. 若点A(-5,y1),B(-2,y2)都在直线y=- x上,则y1y2(填“>”或“<”).14. 如图,在△ABC中,BD⊥AC于D,点E为AB的中点,AD=6,DE=5,则线段BD的长等于 .
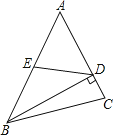 15. 在▱ABCD中,对角线AC,BD交于点O,AC=8,BD=12,则AD的取值范围是.16. 如图,在矩形 中, , , 是 边的中点, 是线段 的动点,将 沿 所在直线折叠得到 ,连接 ,则 的最小值是.
15. 在▱ABCD中,对角线AC,BD交于点O,AC=8,BD=12,则AD的取值范围是.16. 如图,在矩形 中, , , 是 边的中点, 是线段 的动点,将 沿 所在直线折叠得到 ,连接 ,则 的最小值是.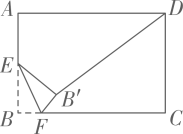 17. 如图,正方形 的边长为 ,点 为 边上一点, ,点 为 的中点,过点 作直线分别与 , 相交于点 , .若 ,则 长为 .
17. 如图,正方形 的边长为 ,点 为 边上一点, ,点 为 的中点,过点 作直线分别与 , 相交于点 , .若 ,则 长为 .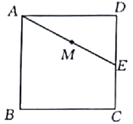 18. 如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点.点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足是F,连接OF,则OF的长为.
18. 如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点.点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足是F,连接OF,则OF的长为.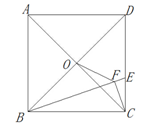
三、解答题
-
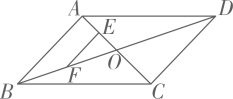
19. 如图, 的对角线 , 相交于 ,点 、 分别是线段 、 的中点.若 厘米, 的周长是 厘米,求 的长.
 20. 小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系式示意图.根据图中提供的信息回答下列问题:
20. 小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系式示意图.根据图中提供的信息回答下列问题: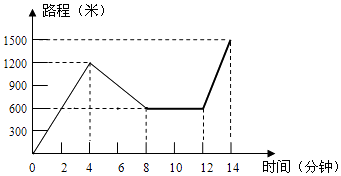 (1)、小红家到舅舅家的路程是米,小红在商店停留了分钟;(2)、在整个去舅舅家的途中哪个时间段小红骑车速度最快,最快的速度是多少米分?(3)、本次去舅舅家的行程中,小红一共行驶了多少米?一共用了多少分钟?21. 如图,在四边形ABCD中,对角线AC、BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10;
(1)、小红家到舅舅家的路程是米,小红在商店停留了分钟;(2)、在整个去舅舅家的途中哪个时间段小红骑车速度最快,最快的速度是多少米分?(3)、本次去舅舅家的行程中,小红一共行驶了多少米?一共用了多少分钟?21. 如图,在四边形ABCD中,对角线AC、BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10;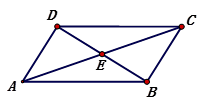 (1)、求证:四边形ABCD是平行四边形.(2)、求四边形ABCD的面积.22. 已知 与 成正比例,且 时, .(1)、写出 与 之间的函数关系(2)、计算 时, 的值;(3)、计算 时, 的值;(4)、若点 在这个函数图象上,求 的值.23. 如图,已知平行四边形 ,延长 到 ,使 ,连接 与 交于 点.
(1)、求证:四边形ABCD是平行四边形.(2)、求四边形ABCD的面积.22. 已知 与 成正比例,且 时, .(1)、写出 与 之间的函数关系(2)、计算 时, 的值;(3)、计算 时, 的值;(4)、若点 在这个函数图象上,求 的值.23. 如图,已知平行四边形 ,延长 到 ,使 ,连接 与 交于 点.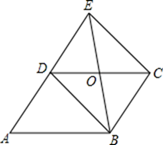 (1)、求证: ;(2)、当 时,连续 , ,求证:四边形 为矩形.24. 菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)、求证: ;(2)、当 时,连续 , ,求证:四边形 为矩形.24. 菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.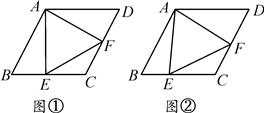 (1)、如图①,若点E是BC的中点,∠AEF=60°,求证:BE=DF;(2)、如图②,若∠EAF=60°,求证:△AEF是等边三角形.25. 如图1,在正方形 中,点 为 上一点,连接 ,把 沿 折叠得到 ,延长 交 于 ,连接 .
(1)、如图①,若点E是BC的中点,∠AEF=60°,求证:BE=DF;(2)、如图②,若∠EAF=60°,求证:△AEF是等边三角形.25. 如图1,在正方形 中,点 为 上一点,连接 ,把 沿 折叠得到 ,延长 交 于 ,连接 .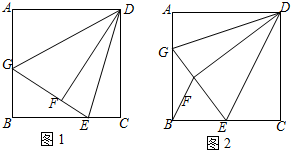 (1)、求 的度数.(2)、如图 , 为 的中点,连接 .
(1)、求 的度数.(2)、如图 , 为 的中点,连接 .①求证: ;
②若正方形边长为 ,求线段 的长.
26. 如图,平行四边形 中, , , ,点 与点 是平行四边形 边上的动点,点 以每秒 个单位长度的速度,从点 运动到点 ,点 以每秒 个单位长度的速度从点 →点 →点 运动.当其中一个点到达终点时,另一个随之停止运动.点 与点 同时出发,设运动时间为 , 的面积为 .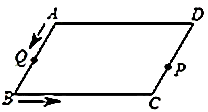 (1)、求 关于 的函数关系式;(2)、 为何值时,将 以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.
(1)、求 关于 的函数关系式;(2)、 为何值时,将 以它的一边为轴翻折,翻折前后的两个三角形所组成的四边形为菱形.